hw3: done all but 1.5 and 2.5
This commit is contained in:
parent
ca2a294fc7
commit
421192b7e5
18 changed files with 361 additions and 84819 deletions
|
|
@ -1,4 +1,4 @@
|
|||
%% Homework 2 - Optimization Methods
|
||||
0%% Homework 2 - Optimization Methods
|
||||
% Author: Claudio Maggioni
|
||||
%
|
||||
% Note: exercises are not in the right order due to matlab constraints of
|
||||
|
|
|
|||
BIN
Claudio_Maggioni_3/1-4-grad-large.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-grad-large.jpg
Normal file
Binary file not shown.
|
After 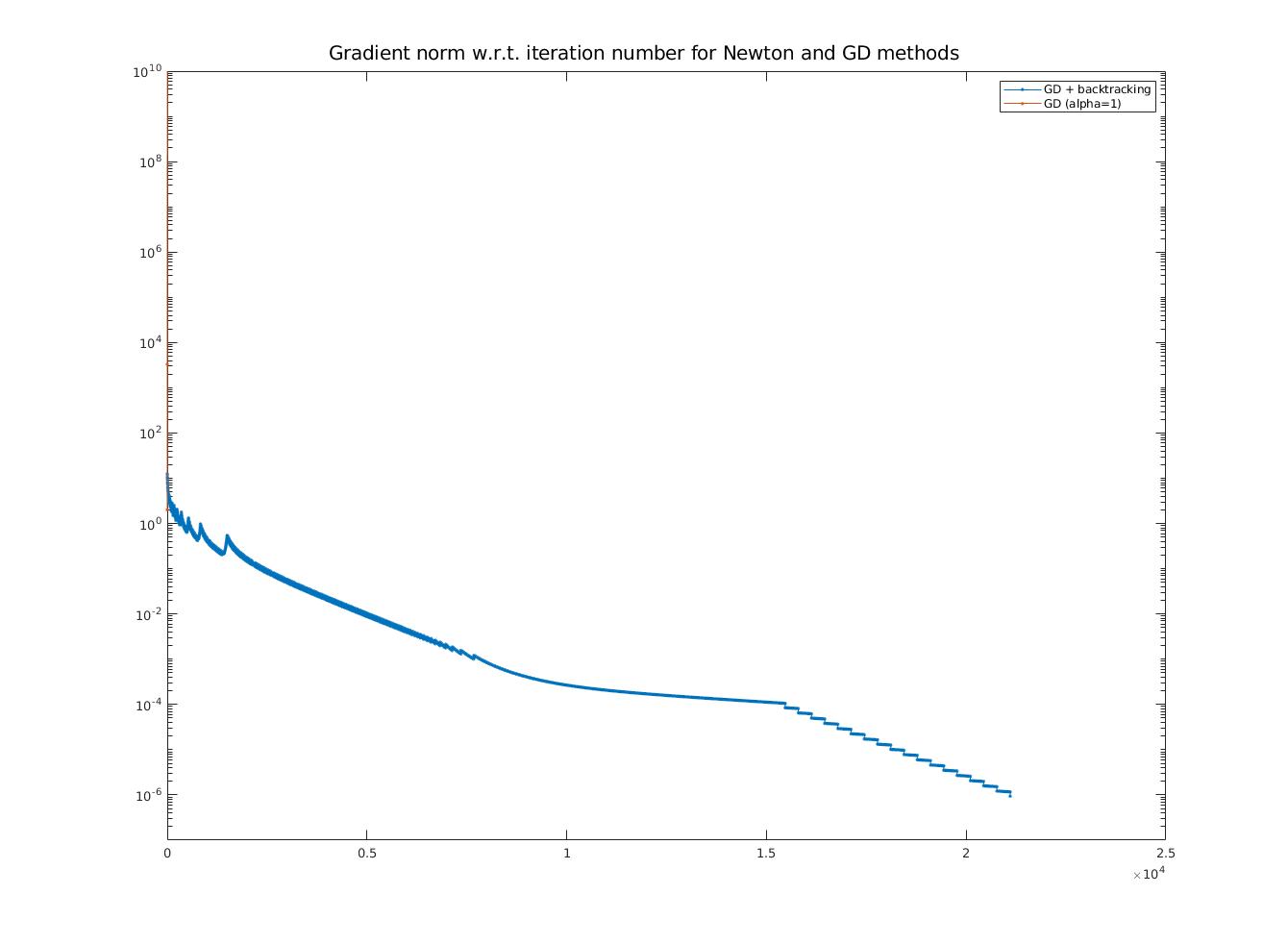
(image error) Size: 51 KiB |
BIN
Claudio_Maggioni_3/1-4-grad-nonlog.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-grad-nonlog.jpg
Normal file
Binary file not shown.
|
After 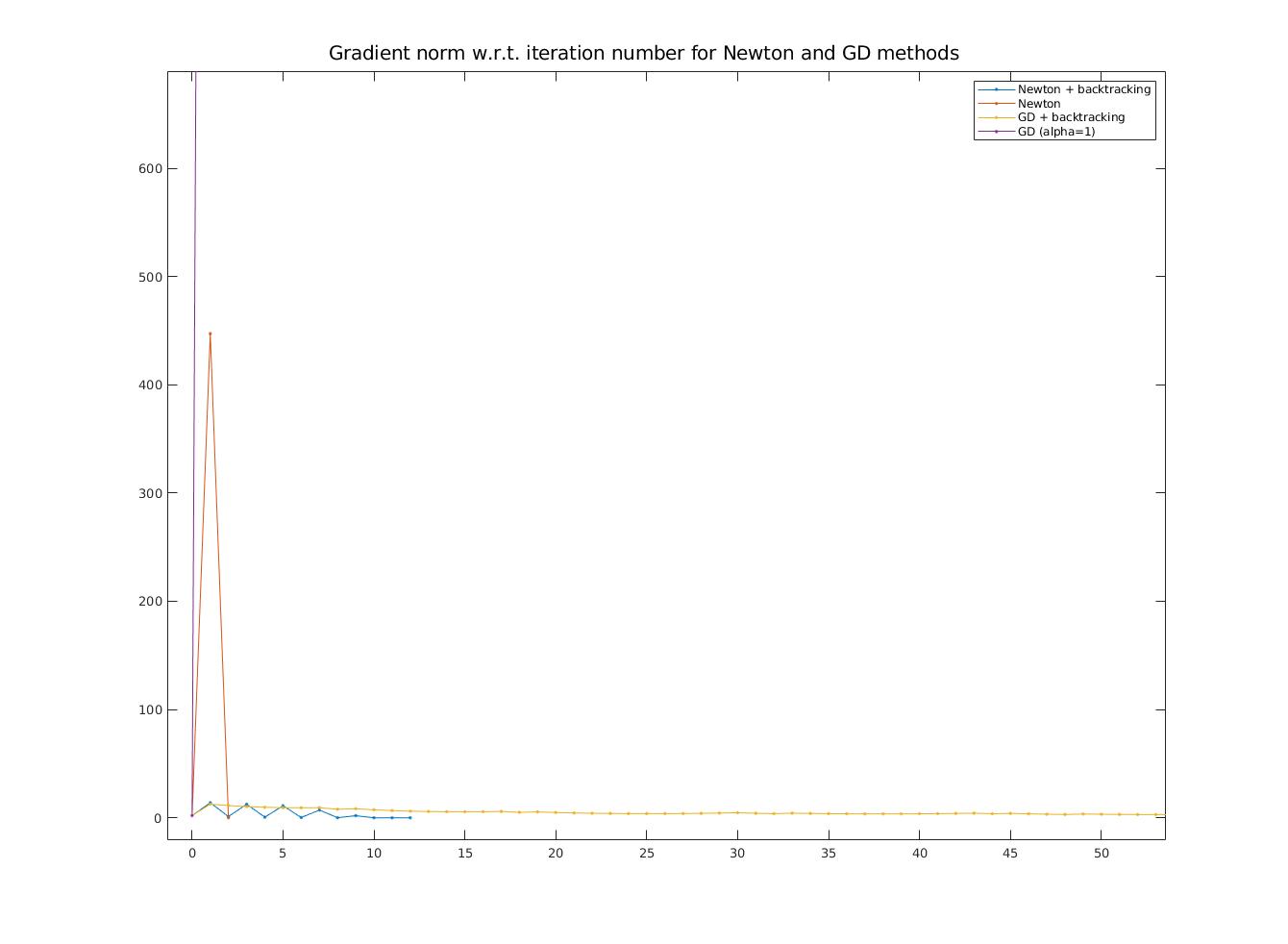
(image error) Size: 49 KiB |
BIN
Claudio_Maggioni_3/1-4-grad.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-grad.jpg
Normal file
Binary file not shown.
|
After 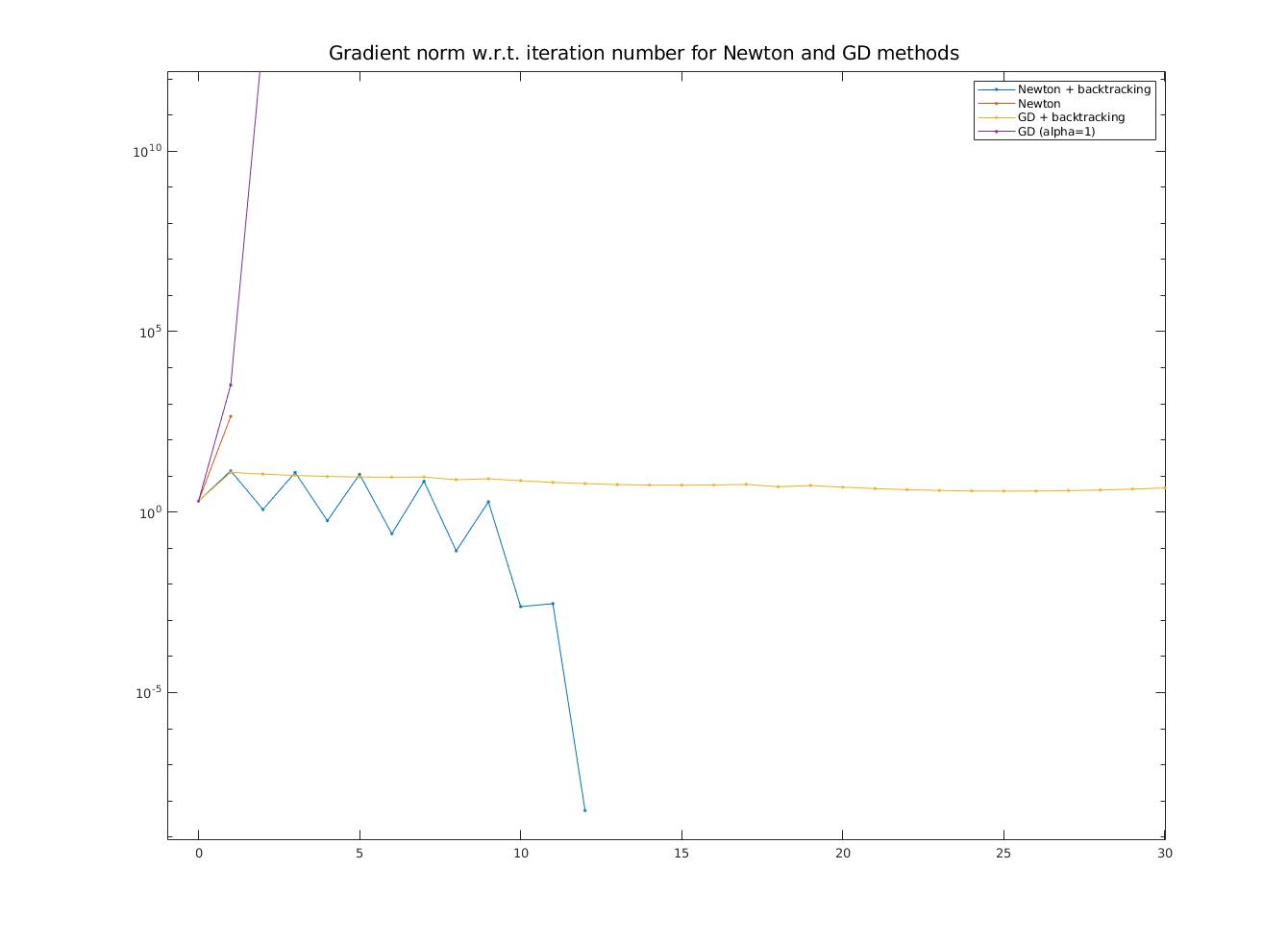
(image error) Size: 49 KiB |
BIN
Claudio_Maggioni_3/1-4-ys-large.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-ys-large.jpg
Normal file
Binary file not shown.
|
After 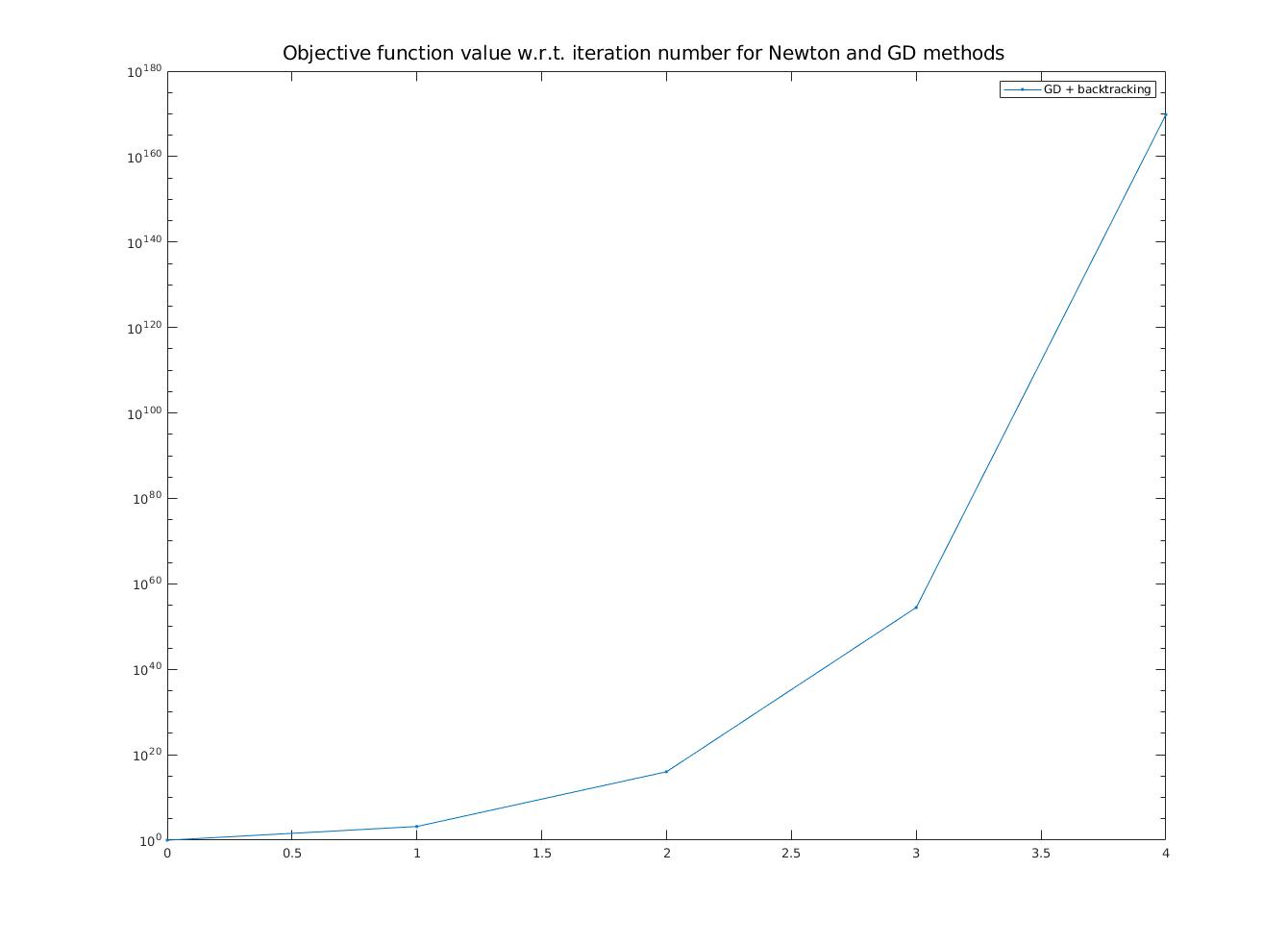
(image error) Size: 48 KiB |
BIN
Claudio_Maggioni_3/1-4-ys-nonlog.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-ys-nonlog.jpg
Normal file
Binary file not shown.
|
After 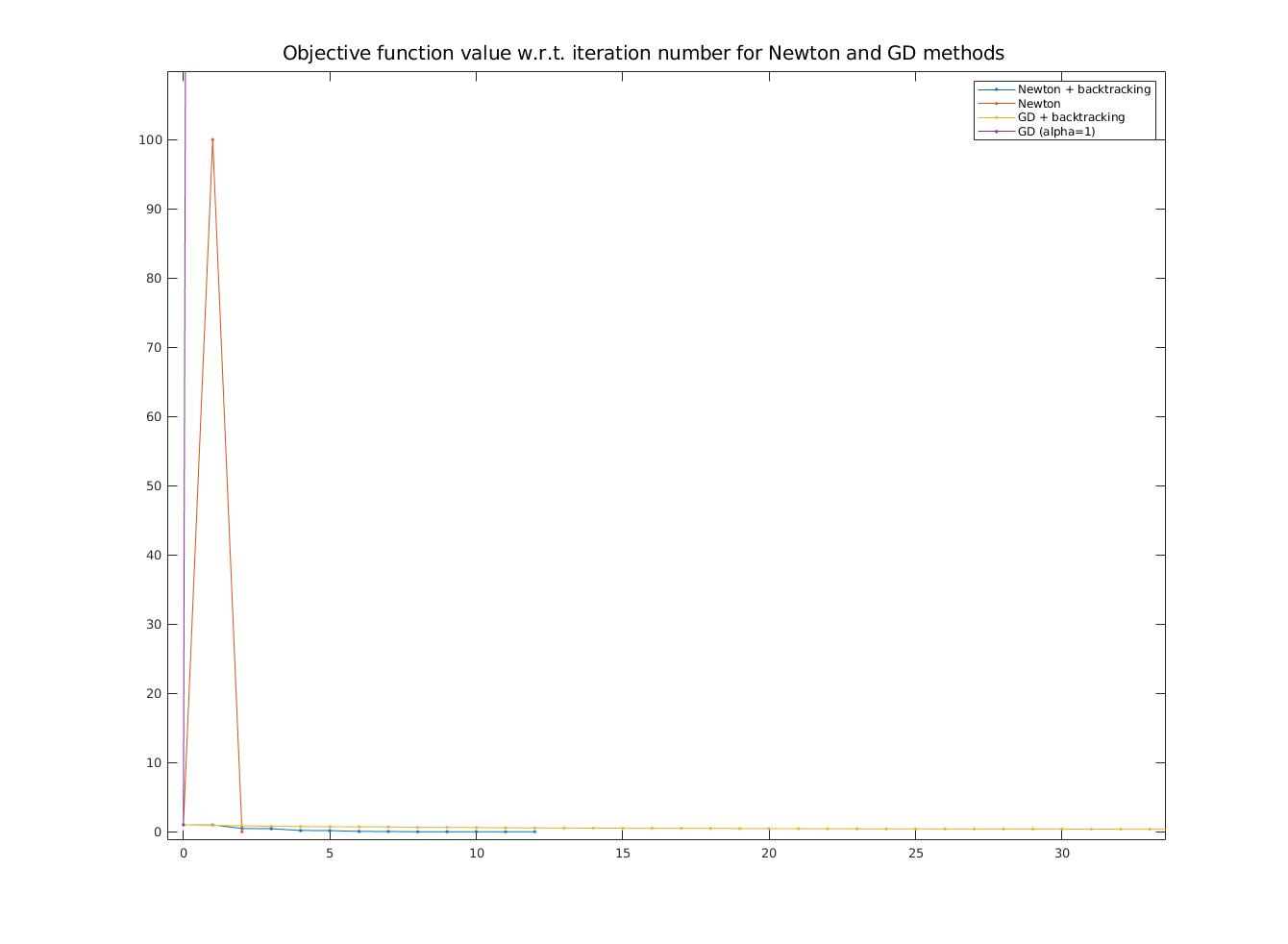
(image error) Size: 50 KiB |
BIN
Claudio_Maggioni_3/1-4-ys.jpg
Normal file
BIN
Claudio_Maggioni_3/1-4-ys.jpg
Normal file
Binary file not shown.
|
After 
(image error) Size: 49 KiB |
BIN
Claudio_Maggioni_3/Claudio_Maggioni_3.pdf
Normal file
BIN
Claudio_Maggioni_3/Claudio_Maggioni_3.pdf
Normal file
Binary file not shown.
147
Claudio_Maggioni_3/Claudio_Maggioni_3.tex
Executable file
147
Claudio_Maggioni_3/Claudio_Maggioni_3.tex
Executable file
|
|
@ -0,0 +1,147 @@
|
|||
\documentclass{scrartcl}
|
||||
\usepackage{pdfpages}
|
||||
\usepackage[utf8]{inputenc}
|
||||
\usepackage{float}
|
||||
\usepackage{graphicx}
|
||||
\usepackage[ruled,vlined]{algorithm2e}
|
||||
\usepackage{subcaption}
|
||||
\usepackage{hyperref}
|
||||
\usepackage{amsmath}
|
||||
\usepackage{pgfplots}
|
||||
\pgfplotsset{compat=newest}
|
||||
\usetikzlibrary{plotmarks}
|
||||
\usetikzlibrary{arrows.meta}
|
||||
\usepgfplotslibrary{patchplots}
|
||||
\usepackage{grffile}
|
||||
\usepackage{amsmath}
|
||||
\usepackage{subcaption}
|
||||
\usepgfplotslibrary{external}
|
||||
\tikzexternalize
|
||||
\usepackage[margin=2.5cm]{geometry}
|
||||
|
||||
% To compile:
|
||||
% sed -i 's#title style={font=\\bfseries#title style={yshift=1ex, font=\\tiny\\bfseries#' *.tex
|
||||
% luatex -enable-write18 -shellescape main.tex
|
||||
|
||||
\pgfplotsset{every x tick label/.append style={font=\tiny, yshift=0.5ex}}
|
||||
\pgfplotsset{every title/.append style={font=\tiny, align=center}}
|
||||
\pgfplotsset{every y tick label/.append style={font=\tiny, xshift=0.5ex}}
|
||||
\pgfplotsset{every z tick label/.append style={font=\tiny, xshift=0.5ex}}
|
||||
|
||||
\setlength{\parindent}{0cm}
|
||||
\setlength{\parskip}{0.5\baselineskip}
|
||||
|
||||
\title{Optimization methods -- Homework 3}
|
||||
\author{Claudio Maggioni}
|
||||
|
||||
\begin{document}
|
||||
|
||||
\maketitle
|
||||
|
||||
\section{Exercise 1}
|
||||
|
||||
\subsection{Exercise 1.1}
|
||||
|
||||
Please consult the MATLAB implementation in the files \texttt{Newton.m}, \texttt{GD.m}, and \texttt{backtracking.m}.
|
||||
Please note that, for this and subsequent exercises, the gradient descent method without backtracking activated uses a
|
||||
fixed $\alpha=1$ despite the indications on the assignment sheet. This was done in order to comply with the forum post
|
||||
on iCorsi found here: \url{https://www.icorsi.ch/mod/forum/discuss.php?d=81144}.
|
||||
|
||||
\subsection{Exercise 1.2}
|
||||
|
||||
Please consult the MATLAB implementation in the file \texttt{main.m} in section 1.2.
|
||||
|
||||
\subsection{Exercise 1.3}
|
||||
|
||||
Please find the requested plots in figure \ref{fig:1}. The code used to generate these plots can be found in section 1.3 of \texttt{main.m}.
|
||||
|
||||
\begin{figure}[h]
|
||||
\begin{subfigure}{0.5\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{ex1-3.jpg}}
|
||||
\caption{Zoomed plot on $x = (-1,1)$ and $y = (-1,1)$}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.5\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\input{ex1-3-gd}}
|
||||
\caption{Complete plot}
|
||||
\end{subfigure}
|
||||
\caption{Steps in the energy landscape for Newton and GD methods}\label{fig:1}
|
||||
\end{figure}
|
||||
|
||||
\subsection{Exercise 1.4}
|
||||
|
||||
Please find the requested plots in figure \ref{fig:gsppn}. The code used to generate these plots can be found in section 1.4 of \texttt{main.m}.
|
||||
|
||||
\begin{figure}[h]
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-grad-nonlog.jpg}}
|
||||
\caption{Gradient norms \\(zoomed, y axis is linear for this plot)}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-ys-nonlog.jpg}}
|
||||
\caption{Objective function values \\(zoomed, y axis is linear for this plot)}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-grad.jpg}}
|
||||
\caption{Gradient norms (zoomed)}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-ys.jpg}}
|
||||
\caption{Objective function values (zoomed)}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-grad-large.jpg}}
|
||||
\caption{Gradient norms}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.45\textwidth}
|
||||
\centering
|
||||
\resizebox{\textwidth}{\textwidth}{\includegraphics{1-4-ys-large.jpg}}
|
||||
\caption{Objective function values}
|
||||
\end{subfigure}
|
||||
\caption{Gradient norms and objective function values (y-axes) w.r.t. iteration numbers (x-axis) for Newton and GD methods (y-axis is log scaled, points at $y=0$ not shown due to log scale)}\label{fig:gsppn}
|
||||
\end{figure}
|
||||
|
||||
\section{Exercise 1.5}
|
||||
|
||||
TBD
|
||||
|
||||
\section{Exercise 2}
|
||||
|
||||
\subsection{Exercise 2.1}
|
||||
|
||||
Please consult the MATLAB implementation in the file \texttt{BGFS.m}.
|
||||
|
||||
\subsection{Exercise 2.2}
|
||||
|
||||
Please consult the MATLAB implementation in the file \texttt{main.m} in section 2.2.
|
||||
|
||||
\subsection{Exercise 2.3}
|
||||
|
||||
Please find the requested plots in figure \ref{fig:3}. The code used to generate these plots can be found in section 2.3 of \texttt{main.m}.
|
||||
|
||||
\begin{figure}[h]
|
||||
\centering
|
||||
\resizebox{.6\textwidth}{.6\textwidth}{\input{ex2-3}}
|
||||
\caption{Steps in the energy landscape for BGFS method}\label{fig:3}
|
||||
\end{figure}
|
||||
|
||||
\subsection{Exercise 2.4}
|
||||
|
||||
Please find the requested plots in figure \ref{fig:4}. The code used to generate these plots can be found in section 2.4 of \texttt{main.m}.
|
||||
|
||||
\begin{figure}[h]
|
||||
\begin{subfigure}{0.5\textwidth}`
|
||||
\resizebox{\textwidth}{\textwidth}{\input{ex2-4-grad}}
|
||||
\caption{Gradient norms}
|
||||
\end{subfigure}
|
||||
\begin{subfigure}{0.5\textwidth}
|
||||
\resizebox{\textwidth}{\textwidth}{\input{ex2-4-ys}}
|
||||
\caption{Objective function values}
|
||||
\end{subfigure}
|
||||
\caption{Gradient norms and objective function values (y-axes) w.r.t. iteration numbers (x-axis) for BFGS method (y-axis is log scaled, points at $y=0$ not shown due to log scale)}\label{fig:4}
|
||||
\end{figure}
|
||||
|
||||
\subsection{Exercise 2.5}
|
||||
|
||||
TBD
|
||||
|
||||
\end{document}
|
||||
|
|
@ -1,34 +0,0 @@
|
|||
% This file was created by matlab2tikz.
|
||||
%
|
||||
\definecolor{mycolor1}{rgb}{0.00000,0.44700,0.74100}%
|
||||
%
|
||||
\begin{tikzpicture}
|
||||
|
||||
\begin{axis}[%
|
||||
width=4.617in,
|
||||
height=3.641in,
|
||||
at={(0.774in,0.491in)},
|
||||
scale only axis,
|
||||
unbounded coords=jump,
|
||||
xmin=-5e+127,
|
||||
xmax=3e+128,
|
||||
ymin=0,
|
||||
ymax=1.8e+86,
|
||||
axis background/.style={fill=white},
|
||||
legend style={legend cell align=left, align=left, draw=white!15!black}
|
||||
]
|
||||
\addplot [color=mycolor1, mark=*, mark options={solid, mycolor1}]
|
||||
table[row sep=crcr]{%
|
||||
0 0\\
|
||||
2 0\\
|
||||
-3200 800\\
|
||||
13106176003202 2047840800\\
|
||||
-9.00508836393827e+41 3.43543698853816e+28\\
|
||||
2.92094868655132e+128 1.62183232884673e+86\\
|
||||
-inf 1.70638824589317e+259\\
|
||||
nan inf\\
|
||||
};
|
||||
\addlegendentry{GD (alpha=1)}
|
||||
|
||||
\end{axis}
|
||||
\end{tikzpicture}%
|
||||
BIN
Claudio_Maggioni_3/ex1-3.jpg
Normal file
BIN
Claudio_Maggioni_3/ex1-3.jpg
Normal file
Binary file not shown.
|
After 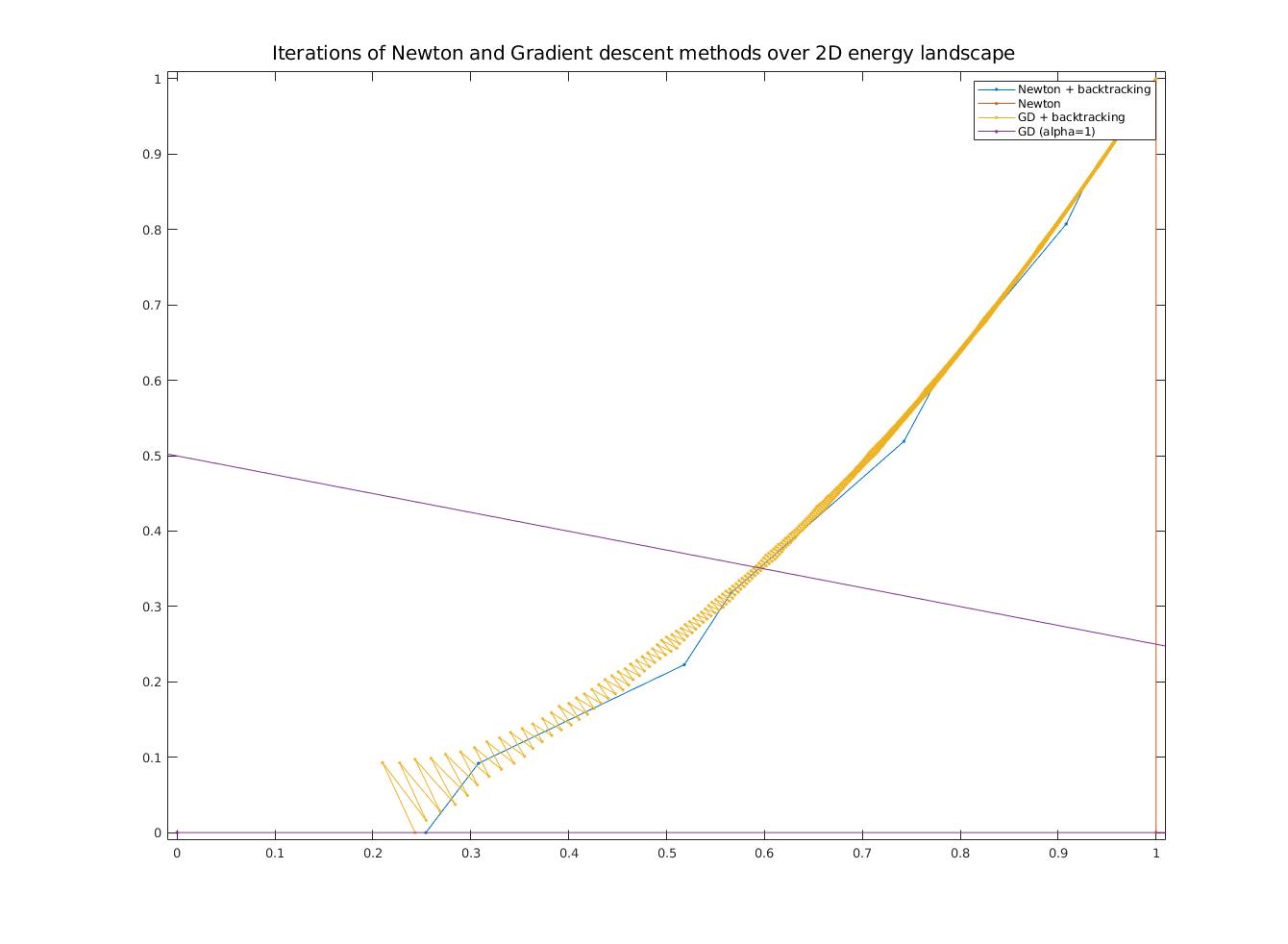
(image error) Size: 61 KiB |
File diff suppressed because it is too large
Load diff
File diff suppressed because it is too large
Load diff
File diff suppressed because it is too large
Load diff
|
|
@ -1,36 +0,0 @@
|
|||
% This file was created by matlab2tikz.
|
||||
%
|
||||
\definecolor{mycolor1}{rgb}{0.00000,0.44700,0.74100}%
|
||||
%
|
||||
\begin{tikzpicture}
|
||||
|
||||
\begin{axis}[%
|
||||
width=4.617in,
|
||||
height=3.641in,
|
||||
at={(0.774in,0.491in)},
|
||||
scale only axis,
|
||||
unbounded coords=jump,
|
||||
xmin=0,
|
||||
xmax=4,
|
||||
ymode=log,
|
||||
ymin=1,
|
||||
ymax=1e+200,
|
||||
yminorticks=true,
|
||||
axis background/.style={fill=white},
|
||||
legend style={legend cell align=left, align=left, draw=white!15!black}
|
||||
]
|
||||
\addplot [color=mycolor1, mark=*, mark options={solid, mycolor1}]
|
||||
table[row sep=crcr]{%
|
||||
0 1\\
|
||||
1 1601\\
|
||||
2 1.04841216742464e+16\\
|
||||
3 2.95055682555403e+54\\
|
||||
4 6.57585025723101e+169\\
|
||||
5 inf\\
|
||||
6 inf\\
|
||||
7 nan\\
|
||||
};
|
||||
\addlegendentry{GD + backtracking}
|
||||
|
||||
\end{axis}
|
||||
\end{tikzpicture}%
|
||||
File diff suppressed because it is too large
Load diff
176
Claudio_Maggioni_3/main.asv
Normal file
176
Claudio_Maggioni_3/main.asv
Normal file
|
|
@ -0,0 +1,176 @@
|
|||
%% Homework 3 - Optimization Methods
|
||||
% Author: Claudio Maggioni
|
||||
%
|
||||
% Note: exercises are not in the right order due to matlab constraints of
|
||||
% functions inside of scripts.
|
||||
|
||||
clc
|
||||
clear
|
||||
close all
|
||||
|
||||
% Set to non-zero to generate LaTeX for graphs
|
||||
enable_m2tikz = 0;
|
||||
if enable_m2tikz
|
||||
addpath /home/claudio/git/matlab2tikz/src
|
||||
else
|
||||
matlab2tikz = @(a,b,c) 0;
|
||||
end
|
||||
|
||||
syms x y;
|
||||
f = (1 - x)^2 + 100 * (y - x^2)^2;
|
||||
global fl
|
||||
fl = matlabFunction(f);
|
||||
|
||||
%% 1.3 - Newton and GD solutions and energy plot
|
||||
|
||||
[x1, xs1, gs1] = Newton(f, [0;0], 50000, 1e-6, true);
|
||||
plot(xs1(1, :), xs1(2, :), 'Marker', '.');
|
||||
fprintf("Newton backtracking: it=%d\n", size(xs1, 2)-1);
|
||||
xlim([-0.01 1.01])
|
||||
ylim([-0.01 1.01])
|
||||
hold on;
|
||||
[x2, xs2, gs2] = Newton(f, [0;0], 50000, 1e-6, false);
|
||||
plot(xs2(1, :), xs2(2, :), 'Marker', '.');
|
||||
fprintf("Newton: it=%d\n", size(xs2, 2)-1);
|
||||
|
||||
[x3, xs3, gs3] = GD(f, [0;0], 50000, 1e-6, true);
|
||||
plot(xs3(1, :), xs3(2, :), 'Marker', '.');
|
||||
fprintf("GD backtracking: it=%d\n", size(xs3, 2)-1);
|
||||
|
||||
[x4, xs4, gs4] = GD(f, [0;0], 50000, 1e-6, false);
|
||||
plot(xs4(1, :), xs4(2, :), 'Marker', '.');
|
||||
fprintf("GD: it=%d\n", size(xs4, 2)-1);
|
||||
hold off;
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Iterations of Newton and Gradient descent methods over 2D energy landscape");
|
||||
matlab2tikz('showInfo', false, './ex1-3.tex');
|
||||
|
||||
figure;
|
||||
plot(xs4(1, :), xs4(2, :), 'Marker', '.');
|
||||
legend('GD (alpha=1)')
|
||||
sgtitle("Iterations of Newton and Gradient descent methods over 2D energy landscape");
|
||||
matlab2tikz('showInfo', false, './ex1-3-large.tex');
|
||||
|
||||
%% 2.3 - BGFS solution and energy plot
|
||||
|
||||
figure;
|
||||
[x5, xs5, gs5] = BGFS(f, [0;0], eye(2), 50000, 1e-6);
|
||||
xlim([-0.01 1.01])
|
||||
ylim([-0.01 1.01])
|
||||
plot(xs5(1, :), xs5(2, :), 'Marker', '.');
|
||||
fprintf("BGFS backtracking: it=%d\n", size(xs5, 2)-1);
|
||||
|
||||
sgtitle("Iterations of BGFS method over 2D energy landscape");
|
||||
matlab2tikz('showInfo', false, './ex2-3.tex');
|
||||
|
||||
%% 1.4 - Newton and GD gradient norm log
|
||||
|
||||
figure;
|
||||
semilogy(0:size(xs1, 2)-1, gs1, 'Marker', '.');
|
||||
ylim([5e-10, 1e12]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
semilogy(0:size(xs2, 2)-1, gs2, 'Marker', '.');
|
||||
semilogy(0:size(xs3, 2)-1, gs3, 'Marker', '.');
|
||||
semilogy(0:size(xs4, 2)-1, gs4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Gradient norm w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-grad.tex');
|
||||
|
||||
|
||||
figure;
|
||||
plot(0:size(xs1, 2)-1, gs1, 'Marker', '.');
|
||||
ylim([5e-10, 25]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
plot(0:size(xs2, 2)-1, gs2, 'Marker', '.');
|
||||
plot(0:size(xs3, 2)-1, gs3, 'Marker', '.');
|
||||
plot(0:size(xs4, 2)-1, gs4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Gradient norm w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-grad.tex');
|
||||
|
||||
figure;
|
||||
semilogy(0:size(xs3, 2)-1, gs3, 'Marker', '.');
|
||||
ylim([1e-7, 1e10]);
|
||||
hold on
|
||||
semilogy(0:size(xs4, 2)-1, gs4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Gradient norm w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-grad-large.tex');
|
||||
|
||||
figure;
|
||||
ys1 = funvalues(xs1);
|
||||
ys2 = funvalues(xs2);
|
||||
ys3 = funvalues(xs3);
|
||||
ys4 = funvalues(xs4);
|
||||
ys5 = funvalues(xs5);
|
||||
semilogy(0:size(xs1, 2)-1, ys1, 'Marker', '.');
|
||||
ylim([5e-19, 1e12]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
semilogy(0:size(xs2, 2)-1, ys2, 'Marker', '.');
|
||||
semilogy(0:size(xs3, 2)-1, ys3, 'Marker', '.');
|
||||
semilogy(0:size(xs4, 2)-1, ys4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Objective function value w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-ys.tex');
|
||||
|
||||
ys1 = funvalues(xs1);
|
||||
ys2 = funvalues(xs2);
|
||||
ys3 = funvalues(xs3);
|
||||
ys4 = funvalues(xs4);
|
||||
ys5 = funvalues(xs5);
|
||||
semilogy(0:size(xs1, 2)-1, ys1, 'Marker', '.');
|
||||
ylim([5e-19, 20]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
semilogy(0:size(xs2, 2)-1, ys2, 'Marker', '.');
|
||||
semilogy(0:size(xs3, 2)-1, ys3, 'Marker', '.');
|
||||
semilogy(0:size(xs4, 2)-1, ys4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Objective function value w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-ys.tex');
|
||||
|
||||
figure;
|
||||
|
||||
semilogy(0:size(xs3, 2)-1, ys3, 'Marker', '.');
|
||||
semilogy(0:size(xs4, 2)-1, ys4, 'Marker', '.');
|
||||
|
||||
legend('GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Objective function value w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-ys-large.tex');
|
||||
|
||||
%% 2.4 - BGFS gradient norms plot
|
||||
|
||||
figure;
|
||||
semilogy(0:size(xs5, 2)-1, gs5, 'Marker', '.');
|
||||
|
||||
sgtitle("Gradient norm w.r.t. iteration number for BGFS method");
|
||||
matlab2tikz('showInfo', false, './ex2-4-grad.tex');
|
||||
|
||||
%% 2.4 - BGFS objective values plot
|
||||
|
||||
figure;
|
||||
semilogy(0:size(xs5, 2)-1, ys5, 'Marker', '.');
|
||||
|
||||
sgtitle("Objective function value w.r.t. iteration number for BGFS methods");
|
||||
matlab2tikz('showInfo', false, './ex2-4-ys.tex');
|
||||
|
||||
function ys = funvalues(xs)
|
||||
ys = zeros(1, size(xs, 2));
|
||||
global fl
|
||||
for i = 1:size(xs, 2)
|
||||
ys(i) = fl(xs(1,i), xs(2,i));
|
||||
end
|
||||
end
|
||||
|
|
@ -9,7 +9,7 @@ clear
|
|||
close all
|
||||
|
||||
% Set to non-zero to generate LaTeX for graphs
|
||||
enable_m2tikz = 1;
|
||||
enable_m2tikz = 0;
|
||||
if enable_m2tikz
|
||||
addpath /home/claudio/git/matlab2tikz/src
|
||||
else
|
||||
|
|
@ -21,23 +21,26 @@ f = (1 - x)^2 + 100 * (y - x^2)^2;
|
|||
global fl
|
||||
fl = matlabFunction(f);
|
||||
|
||||
%% 1.3 - Newton and GD solutions and energy plot
|
||||
%% 1.2 - Minimizing the Rosenbrock function
|
||||
|
||||
[x1, xs1, gs1] = Newton(f, [0;0], 50000, 1e-6, true);
|
||||
[x2, xs2, gs2] = Newton(f, [0;0], 50000, 1e-6, false);
|
||||
[x3, xs3, gs3] = GD(f, [0;0], 50000, 1e-6, true);
|
||||
[x4, xs4, gs4] = GD(f, [0;0], 50000, 1e-6, false);
|
||||
|
||||
%% 1.3 - Newton and GD solutions and energy plot
|
||||
|
||||
plot(xs1(1, :), xs1(2, :), 'Marker', '.');
|
||||
fprintf("Newton backtracking: it=%d\n", size(xs1, 2)-1);
|
||||
xlim([-0.01 1.01])
|
||||
ylim([-0.01 1.01])
|
||||
hold on;
|
||||
[x2, xs2, gs2] = Newton(f, [0;0], 50000, 1e-6, false);
|
||||
plot(xs2(1, :), xs2(2, :), 'Marker', '.');
|
||||
fprintf("Newton: it=%d\n", size(xs2, 2)-1);
|
||||
|
||||
[x3, xs3, gs3] = GD(f, [0;0], 50000, 1e-6, true);
|
||||
plot(xs3(1, :), xs3(2, :), 'Marker', '.');
|
||||
fprintf("GD backtracking: it=%d\n", size(xs3, 2)-1);
|
||||
|
||||
[x4, xs4, gs4] = GD(f, [0;0], 50000, 1e-6, false);
|
||||
plot(xs4(1, :), xs4(2, :), 'Marker', '.');
|
||||
fprintf("GD: it=%d\n", size(xs4, 2)-1);
|
||||
hold off;
|
||||
|
|
@ -79,6 +82,21 @@ legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
|||
sgtitle("Gradient norm w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-grad.tex');
|
||||
|
||||
|
||||
figure;
|
||||
plot(0:size(xs1, 2)-1, gs1, 'Marker', '.');
|
||||
ylim([5e-10, 401]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
plot(0:size(xs2, 2)-1, gs2, 'Marker', '.');
|
||||
plot(0:size(xs3, 2)-1, gs3, 'Marker', '.');
|
||||
plot(0:size(xs4, 2)-1, gs4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Gradient norm w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-grad.tex');
|
||||
|
||||
figure;
|
||||
semilogy(0:size(xs3, 2)-1, gs3, 'Marker', '.');
|
||||
ylim([1e-7, 1e10]);
|
||||
|
|
@ -97,7 +115,7 @@ ys3 = funvalues(xs3);
|
|||
ys4 = funvalues(xs4);
|
||||
ys5 = funvalues(xs5);
|
||||
semilogy(0:size(xs1, 2)-1, ys1, 'Marker', '.');
|
||||
ylim([5e-19, 1e12]);
|
||||
ylim([0, 1e12]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
semilogy(0:size(xs2, 2)-1, ys2, 'Marker', '.');
|
||||
|
|
@ -109,6 +127,19 @@ legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
|||
sgtitle("Objective function value w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-ys.tex');
|
||||
|
||||
plot(0:size(xs1, 2)-1, ys1, 'Marker', '.');
|
||||
ylim([0, 101]);
|
||||
xlim([-1, 30]);
|
||||
hold on
|
||||
plot(0:size(xs2, 2)-1, ys2, 'Marker', '.');
|
||||
plot(0:size(xs3, 2)-1, ys3, 'Marker', '.');
|
||||
plot(0:size(xs4, 2)-1, ys4, 'Marker', '.');
|
||||
hold off
|
||||
|
||||
legend('Newton + backtracking', 'Newton', 'GD + backtracking', 'GD (alpha=1)')
|
||||
sgtitle("Objective function value w.r.t. iteration number for Newton and GD methods");
|
||||
matlab2tikz('showInfo', false, './ex1-4-ys.tex');
|
||||
|
||||
figure;
|
||||
|
||||
semilogy(0:size(xs3, 2)-1, ys3, 'Marker', '.');
|
||||
|
|
|
|||
Reference in a new issue