| .. | ||
| data | ||
| deliverable | ||
| src | ||
| ex_train_val_test.png | ||
| im.png | ||
| README.md | ||
| report_Maggioni_Claudio.md | ||
| report_Maggioni_Claudio.pdf | ||
Assignment 1
The assignment is split into two parts: you are asked to solve a regression problem, and answer some questions.
You can use all the books, material, and help you need.
Bear in mind that the questions you are asked are similar to those you may find in the final exam, and are related to very important and fundamental machine learning concepts. As such, sooner or later you will need to learn them to pass the course.
We will give you some feedback afterwards.
Tasks
You have to solve a regression problem. You are given a set of data consisting of input-output pairs (x, y), and you have to build a model to fit this data. We will then evaluate the performance of your model on a different test set.
In order to complete the assignment, you have to address the tasks listed below and submit your solution as a zip file on the iCorsi platform. More details are in the Instructions section below.
T1.
Use the family of models f(x, theta) = theta_0 + theta_1 * x_1 + theta_2 * x_2 + theta_3 * x_1 * x_2 + theta_4 * sin(x_1) to fit the data:
- write in the report the formula of the model substituting parameters theta_0, ..., theta_4 with the estimates you've found;
- evaluate the test performance of your model using the mean squared error as performance measure.
T2.
Consider any family of non-linear models of your choice to address the above regression problem: - evaluate the test performance of your model using the mean squared error as performance measure; - compare your model with the linear regression of task 1. Which one is statistically better?
T3. (Bonus)
In the Github repository of the course, you will find a trained Scikit-learn model that we built using the same dataset you are given. This baseline model is able to achieve a MSE of 0.0194, when evaluated on the test set. You will get extra points if the test performance of your model is better (i.e., the MSE is lower) than ours. Of course, you also have to tell us why you think that your model is better.
In order to complete the assignment, you must submit a zip file on the iCorsi platform containing:
- a PDF file describing how you solved the assignment, covering all the points described above (at most 2500 words, no code!);
- a working example of how to load your trained model from file, and evaluate it;
- the source code you used to build, train, and evaluate your model.
See below for more details.
Questions
Motivate all answers, but keep it short; support the answers with formulas where appropriate.
Q1. Training versus Validation
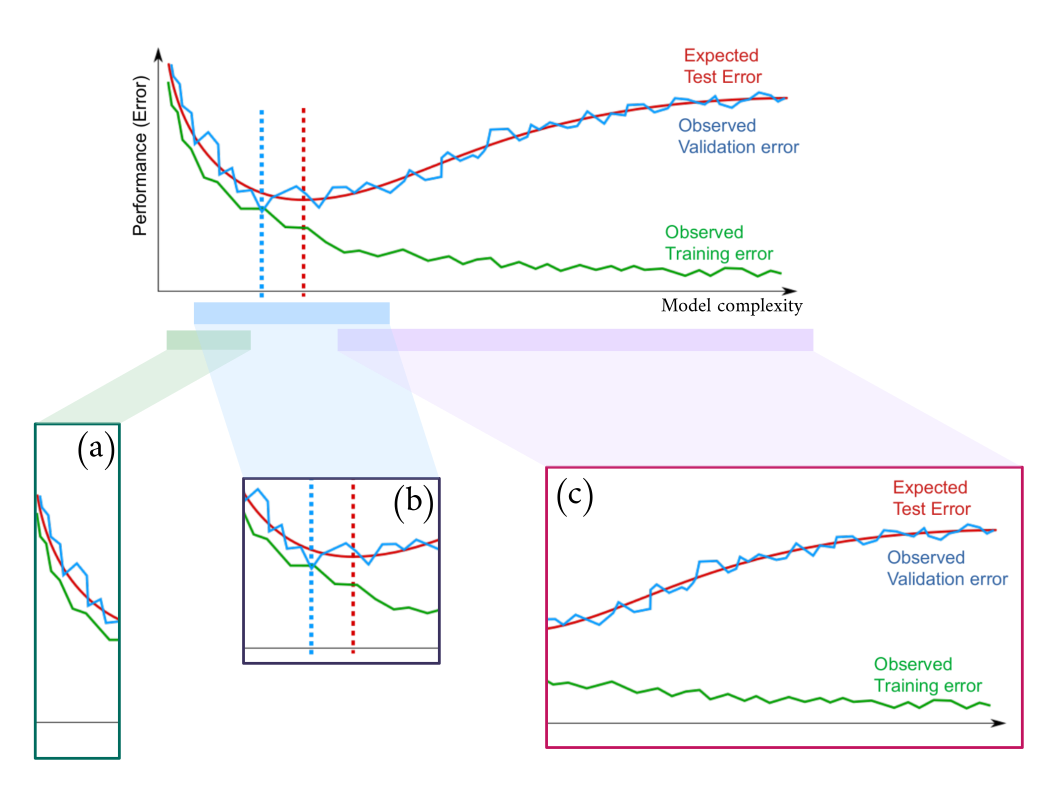
A neural network, trained by gradient descent, is designed to solve a regression problem where the target value is affected by noise. For different complexities of the model family (e.g., varying the number of hidden neurons) the training is performed until convergence (null gradient) and the achieved performance (e.g., mean squared error) is reported in the following plot.
- Explain the curves' behavior in each of the three highlighted sections of the figures, namely (a), (b), and (c);
- Is any of the three section associated with the concepts of overfitting and underfitting? If yes, explain it.
- Is there any evidence of high approximation risk? Why? If yes, in which of the below subfigures?
- Do you think that by further increasing the model complexity you will be able to bring the training error to zero?
- Do you think that by further increasing the model complexity you will be able to bring the structural risk to zero?
Q2. Linear Regression
Consider the following regression problem in which the task is to estimate the target variable y = g(x) + eta, where g(.) is unknown, eta \~ N(0, 1) and the input variable x is a bidimensional vector x = [x_1, x_2].
Suppose to have n training samples and to fit the data using a linear model family f(x, theta) = theta_0 + theta_1 * x_1 + theta_2 * x_2.
Now, we add another regressor (feature) x_3 (to obtain f(x, theta) = theta_0 + theta_1 * x_1 + theta_2 * x_2 + theta_3 * x_3) and we fit a linear model on the same data again. Comment and compare how (a.) the training error, (b.) test error and (c.) coefficients would change in the following cases:
x_3is a normally distributed independent random variable, in particularx_3~ N(1, 2).x_3 = 2.5 * x_1 + x_2.x_3 = x_1 * x_2.
Motivate your answers.
NB: You don't have to run any experiment to answer this question, your answers should be based only on your understanding of linear regression.
Q3. Classification
Consider the classification problem shown in the picture below and answer each point.
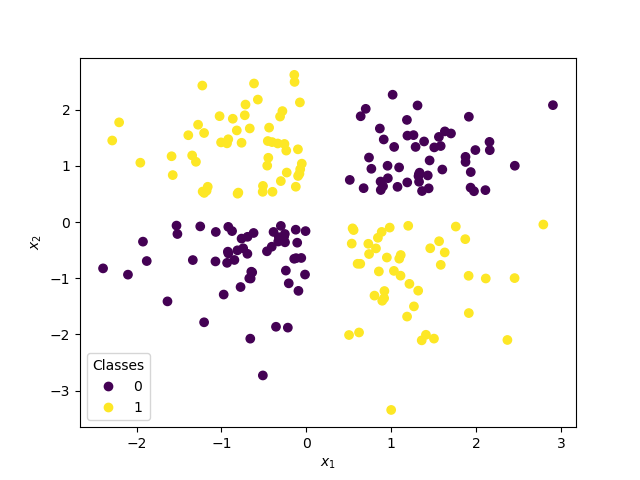
- Your boss asked you to solve the problem using a perceptron and now he's upset because you are getting poor results. How would you justify the poor performance of your perceptron classifier to your boss?
- Would you expect to have better luck with a neural network with activation function
h(x) = - x * e^(-2)for the hidden units? - What are the main differences and similarities between the perceptron and the logistic regression neuron?
Instructions
Tools
Your solution to the regression problem must be entirely coded in Python 3 (not Python 2), using the tools we have seen in the labs.
These include:
- Numpy
- Scikit-learn
- Keras
You can develop your code in Colab, like we saw in the labs, or you can install the libraries on your machine and develop locally.
If you choose to work in Colab, you can then export the code to a .py file by clicking "File > Download .py" in the top menu.
If you want to work locally, instead, you can install Python libraries using something like the Pip package manager. There are plenty of tutorials online.
Submission
In the Github repository of the course, you will find a folder named assignment_1.
The contents of the folder are as follows:
data/:data.npz: a file storing the dataset in a native Numpy format;
deliverable/:run_model.py: a working example of how to evaluate our baseline model;baseline_model.pickle: a binary file storing our baseline model;
src/:utils.py: some utility methods to save and load models;
report_surname_name.pdf: an example of the report;report_surname_name.tex: the LaTeX source for the provided report pdf;
The run_model.py script loads the data from the data folder, loads a model from file, and evaluates the model's MSE on the loaded data.
When evaluating your models on the unseen test set, we will only run this script.
You cannot edit the script, except for the parts necessary to load your model and pre-process the data. Look at the comments in the file to know where you're allowed to edit the code.
You must submit a zip file with a structure similar to the repository, but:
- the
deliverablefolder must contain:run_model.py, edited in order to work with your models;- the saved models for both tasks (linear regression and the model of your choice);
- any additional file to load the trained models and evaluate their performance using
run_model.py;
- the
srcfolder must contain all the source files that your used to build, train, and evaluate your models; - the report must be a pdf file (no need for the
.texfile) covering both the tasks and the questions.
The file should have the following structure:
as1_surname_name/
report_surname_name.pdf
deliverable/
run_model.py
linear_regression.pickle # or any other file storing your linear regression
nonlinear_model.pickle # or any other file storing your model of choice
src/
file1.py
file2.py
...
Remember that we will only execute run_model.py to grade your assignment, so make sure that everything works out of the box.
We don't accept photos or scans of handwritten answers. We strongly suggest you to create your submission in LaTeX (e.g. using Overleaf), so that any formula you may want to write is understandable. Following the .tex sample provided is suggested but not mandatory. You can add figures and tables, where appropriate.
Evaluation criteria
You will get a positive evaluation if:
- you demonstrate a clear understanding of the main tasks and concepts;
- you provide a clear description of your solution to the task;
- you provide sensible motivations for your choice of model and hyper-parameters;
- the statistical comparison between models is conducted appropriately;
- your code runs out of the box (i.e., without us needing to change your code to evaluate the assignment);
- your code is properly commented;
- your model has a good test performance on the unseen data;
- your model has a better test performance than the baseline model provided by us;
- your answers are complete: all the claims are justified, and supported by formulas (where appropriate);
- your answers are re-elaboration of the concepts presented in class, and not only cut-past from a book, Wikipedia or a classmate answer.
You will get a negative evaluation if:
- we realize that you copied your solution (it's important that you explain in your own words, so that it's clear that you understood, even if you discussed your solution with others);
- the description of your solution is not clear, or it incomplete;
- the statistical comparison between models is not thorough;
- your code requires us to edit things manually in order to work;
- your code is not properly commented.