midterm: done w report 1, 2.2-2.5
This commit is contained in:
parent
11ae8556f2
commit
92dac9b00f
5 changed files with 160 additions and 2 deletions
Binary file not shown.
|
Before 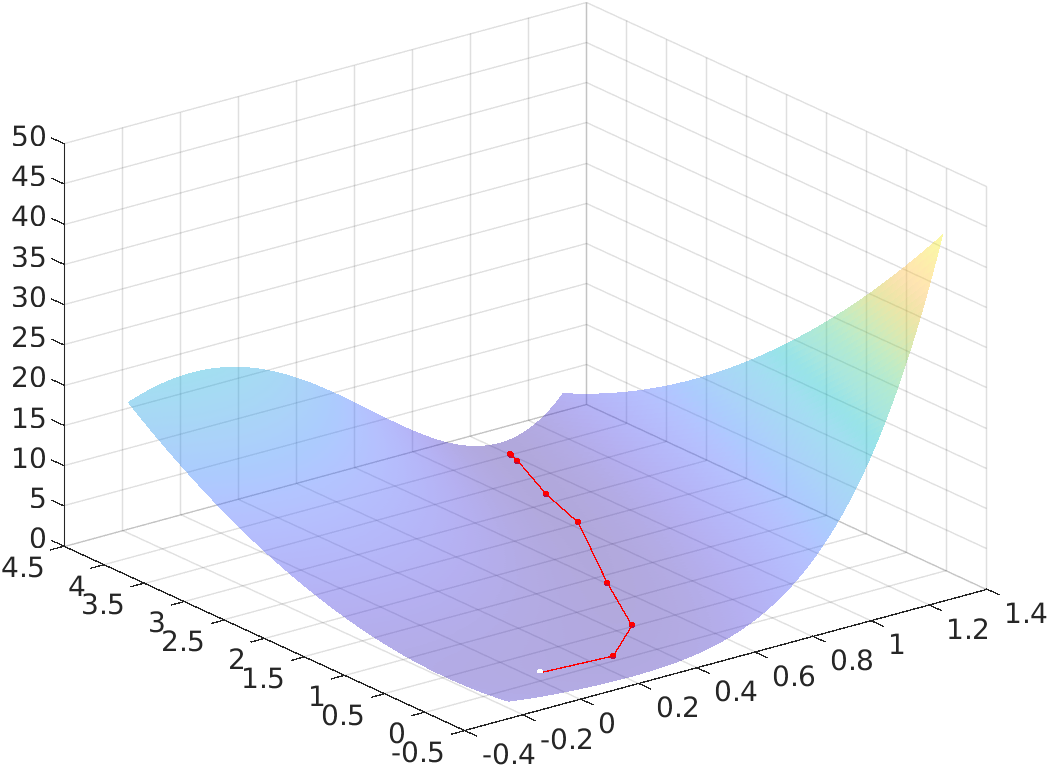
(image error) Size: 142 KiB After 
(image error) Size: 132 KiB 

|
Binary file not shown.
|
Before 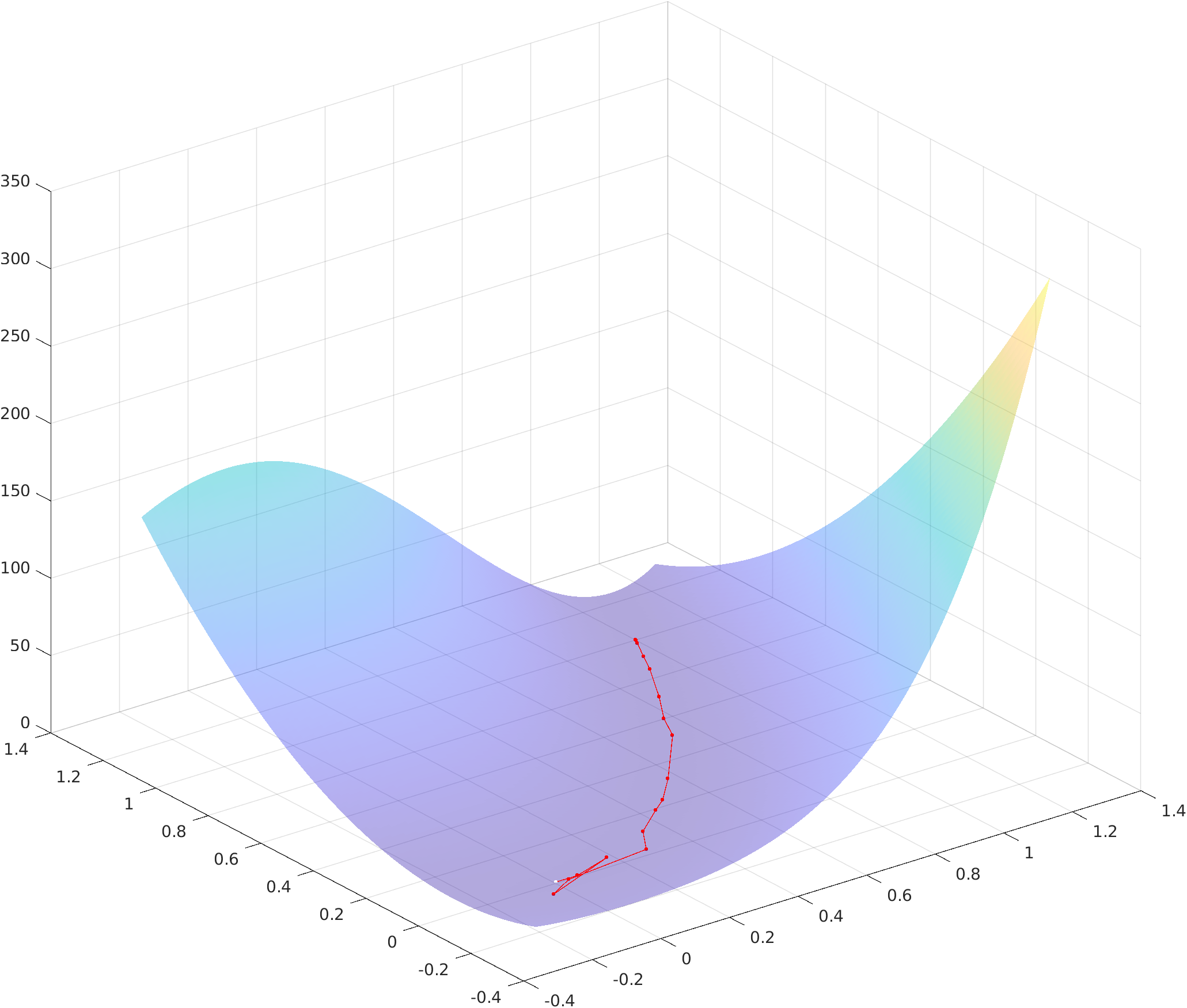
(image error) Size: 307 KiB After 
(image error) Size: 140 KiB 

|
Binary file not shown.
|
Before 
(image error) Size: 58 KiB After 
(image error) Size: 35 KiB 

|
|
|
@ -1,14 +1,18 @@
|
|||
<!-- vim: set ts=2 sw=2 et tw=80: -->
|
||||
|
||||
---
|
||||
title: Midterm -- Optimization Methods
|
||||
author: Claudio Maggioni
|
||||
header-includes:
|
||||
- \usepackage{amsmath}
|
||||
- \usepackage{hyperref}
|
||||
- \usepackage[utf8]{inputenc}
|
||||
- \usepackage[margin=2.5cm]{geometry}
|
||||
- \usepackage[ruled,vlined]{algorithm2e}
|
||||
- \usepackage{float}
|
||||
- \floatplacement{figure}{H}
|
||||
|
||||
---
|
||||
\title{Midterm -- Optimization Methods}
|
||||
\author{Claudio Maggioni}
|
||||
\maketitle
|
||||
|
||||
# Exercise 1
|
||||
|
|
@ -139,3 +143,157 @@ https://en.wikipedia.org/wiki/Definite_matrix#Multiplication)
|
|||
Thanks to this we have indeed proven that the delta $\|e_k\|_A - \|e_{k+1}\|_A$
|
||||
is indeed positive and thus as $i$ increases the energy norm of the error
|
||||
monotonically decreases.
|
||||
|
||||
# Question 2
|
||||
|
||||
## Point 1
|
||||
|
||||
TBD
|
||||
|
||||
## Point 2
|
||||
|
||||
The trust region algorithm is the following:
|
||||
|
||||
\begin{algorithm}[H]
|
||||
\SetAlgoLined
|
||||
Given $\hat{\Delta} > 0, \Delta_0 \in (0,\hat{\Delta})$,
|
||||
and $\eta \in [0, \frac14)$\;
|
||||
|
||||
\For{$k = 0, 1, 2, \ldots$}{%
|
||||
Obtain $p_k$ by using Cauchy or Dogleg method\;
|
||||
$\rho_k \gets \frac{f(x_k) - f(x_k + p_k)}{m_k(0) - m_k(p_k)}$\;
|
||||
\uIf{$\rho_k < \frac14$}{%
|
||||
$\Delta_{k+1} \gets \frac14 \Delta_k$\;
|
||||
}\Else{%
|
||||
\uIf{$\rho_k > \frac34$ and $\|\rho_k\| = \Delta_k$}{%
|
||||
$\Delta_{k+1} \gets \min(2\Delta_k, \hat{\Delta})$\;
|
||||
}
|
||||
\Else{%
|
||||
$\Delta_{k+1} \gets \Delta_k$\;
|
||||
}}
|
||||
\uIf{$\rho_k > \eta$}{%
|
||||
$x_{k+1} \gets x_k + p_k$\;
|
||||
}
|
||||
\Else{
|
||||
$x_{k+1} \gets x_k$\;
|
||||
}
|
||||
}
|
||||
\caption{Trust region method}
|
||||
\end{algorithm}
|
||||
|
||||
The Cauchy point algorithm is the following:
|
||||
|
||||
\begin{algorithm}[H]
|
||||
\SetAlgoLined
|
||||
Input $B$ (quadratic term), $g$ (linear term), $\Delta_k$\;
|
||||
\uIf{$g^T B g \geq 0$}{%
|
||||
$\tau \gets 1$\;
|
||||
}\Else{%
|
||||
$\tau \gets \min(\frac{\|g\|^3}{\Delta_k \cdot g^T B g}, 1)$\;
|
||||
}
|
||||
|
||||
$p_k \gets -\tau \cdot \frac{\Delta_k}{\|g\|^2 \cdot g}$\;
|
||||
\Return{$p_k$}
|
||||
\caption{Cauchy point}
|
||||
\end{algorithm}
|
||||
|
||||
Finally, the Dogleg method algorithm is the following:
|
||||
|
||||
\begin{algorithm}[H]
|
||||
\SetAlgoLined
|
||||
Input $B$ (quadratic term), $g$ (linear term), $\Delta_k$\;
|
||||
$p_N \gets - B^{-1} g$\;
|
||||
|
||||
\uIf{$\|p_N\| < \Delta_k$}{%
|
||||
$p_k \gets p_N$\;
|
||||
}\Else{%
|
||||
$p_u = - \frac{g^T g}{g^T B g} g$\;
|
||||
|
||||
\uIf{$\|p_u\| > \Delta_k$}{%
|
||||
compute $p_k$ with Cauchy point algorithm\;
|
||||
}\Else{%
|
||||
solve for $\tau$ the equality $\|p_u + \tau * (p_N - p_u)\|^2 =
|
||||
\Delta_k^2$\;
|
||||
$p_k \gets p_u + \tau \cdot (p_N - p_u)$\;
|
||||
}
|
||||
}
|
||||
\caption{Dogleg method}
|
||||
\end{algorithm}
|
||||
|
||||
## Point 3
|
||||
|
||||
The trust region, dogleg and Cauchy point algorithms were implemented
|
||||
respectively in the files `trust_region.m`, `dogleg.m`, and `cauchy.m`.
|
||||
|
||||
## Point 4
|
||||
|
||||
### Taylor expansion
|
||||
|
||||
The Taylor expansion up the second order of the function is the following:
|
||||
|
||||
$$f(x_0, w) = f(x_0) + \langle\begin{bmatrix}48x^3 - 16xy + 2x - 2\\2y - 8x^2
|
||||
\end{bmatrix}, w\rangle + \frac12 \langle\begin{bmatrix}144x^2 -16y + 2 - 16 &
|
||||
-16 \\ -16 & 2 \end{bmatrix}w, w\rangle$$
|
||||
|
||||
### Minimization
|
||||
|
||||
The code used to minimize the function can be found in the MATLAB script
|
||||
`main.m` under section 2.4. The resulting minimizer (found in 10 iterations) is:
|
||||
|
||||
$$x_m = \begin{bmatrix}1\\4\end{bmatrix}$$
|
||||
|
||||
### Energy landscape
|
||||
|
||||
The following figure shows a `surf` plot of the objective function overlayed
|
||||
with the iterates used to reach the minimizer:
|
||||
|
||||

|
||||
|
||||
The code used to generate such plot can be found in the MATLAB script `main.m`
|
||||
under section 2.4c.
|
||||
|
||||
## Point 5
|
||||
|
||||
### Minimization
|
||||
|
||||
The code used to minimize the function can be found in the MATLAB script
|
||||
`main.m` under section 2.5. The resulting minimizer (found in 25 iterations) is:
|
||||
|
||||
$$x_m = \begin{bmatrix}1\\5\end{bmatrix}$$
|
||||
|
||||
### Energy landscape
|
||||
|
||||
The following figure shows a `surf` plot of the objective function overlayed
|
||||
with the iterates used to reach the minimizer:
|
||||
|
||||

|
||||
|
||||
The code used to generate such plot can be found in the MATLAB script `main.m`
|
||||
under section 2.5b.
|
||||
|
||||
### Gradient norms
|
||||
|
||||
The following figure shows the logarithm of the norm of the gradient w.r.t.
|
||||
iterations:
|
||||
|
||||

|
||||
|
||||
The code used to generate such plot can be found in the MATLAB script `main.m`
|
||||
under section 2.5c.
|
||||
|
||||
Comparing the behaviour shown above with the figures obtained in the previous
|
||||
assignment for the Newton method with backtracking and the gradient descent with
|
||||
backtracking, we notice that the trust-region method really behaves like a
|
||||
compromise between the two methods. First of all, we notice that TR converges in
|
||||
25 iterations, almost double of the number of iterations of regular NM +
|
||||
backtracking. The actual behaviour of the curve is somewhat similar to the
|
||||
Netwon gradient norms curve w.r.t. to the presence of spikes, which however are
|
||||
less evident in the Trust region curve (probably due to Trust region method
|
||||
alternating quadratic steps with linear or almost linear steps while iterating).
|
||||
Finally, we notice that TR is the only method to have neighbouring iterations
|
||||
having the exact same norm: this is probably due to some proposed iterations
|
||||
steps not being validated by the acceptance criteria, which makes the method mot
|
||||
move for some iterations.
|
||||
|
|
|
|||
Binary file not shown.
Reference in a new issue