OM/Claudio_Maggioni_midterm/Claudio_Maggioni_midterm.md

---

title: Midterm -- Optimization Methods author: Claudio Maggioni header-includes:

• \usepackage{amsmath}
• \usepackage{hyperref}
• \usepackage[utf8]{inputenc}
• \usepackage[margin=2.5cm]{geometry}
• \usepackage[ruled,vlined]{algorithm2e}
• \usepackage{float}
• \floatplacement{figure}{H}
• \hypersetup{colorlinks=true,linkcolor=blue}

---

\maketitle

Acknowledgements on group work

• Gianmarco De Vita suggested me the use of MATLAB's equation solver for parts of dogleg.m's implementation.
• I have discussed my solutions for exercise 1.2 and exercise 3 with several people, namely:
  • Gianmarco De Vita
  • Tommaso Rodolfo Masera
  • Andrea Brites Marto
• This song for the divine inspiration that made me write the proof for Exercise 1.2.

Exercise 1

Point 1

Question (a)

As already covered in the course, the gradient of a standard quadratic form at a point x_0 is equal to:

 \nabla f(x_0) = A x_0 - b 

Plugging in the definition of x_0 and knowing that $\nabla f(x_m) = A x_m - b = 0$ (according to the first necessary condition for a minimizer), we obtain:

\nabla f(x_0) = A (x_m + v) - b = A x_m + A v - b = b + \lambda v - b = \lambda v

Question (b)

The steepest descent method takes exactly one iteration to reach the exact minimizer x_m starting from the point x_0. This can be proven by first noticing that x_m is a point standing in the line that first descent direction would trace, which is equal to:

g(\alpha) = - \alpha \cdot \nabla f(x_0) = - \alpha \lambda v

For \alpha = \frac{1}{\lambda}, and plugging in the definition of $x_0 = x_m + v$, we would reach a new iterate x_1 equal to:

x_1 = x_0 - \alpha \lambda v = x_0 - v = x_m + v - v = x_m 

The only question that we need to answer now is why the SD algorithm would indeed choose \alpha = \frac{1}{\lambda}. To answer this, we recall that the SD algorithm chooses \alpha by solving a linear minimization option along the step direction. Since we know x_m is indeed the minimizer, f(x_m) would be obviously strictly less that any other f(x_1 = x_0 - \alpha \lambda v) with \alpha \neq \frac{1}{\lambda}.

Therefore, since x_1 = x_m, we have proven SD converges to the minimizer in one iteration.

Point 2

The right answer is choice (a), since the energy norm of the error indeed always decreases monotonically.

The proof of this that I will provide is independent from the provided objective or the provided number of iterations, and it works for all choices of A where A is symmetric and positive definite.

Therefore, first of all I will prove A is indeed SPD by computing its eigenvalues.

$$CP(A) = det\left(\begin{bmatrix}2&-1&0\-1&2&-1\0&-1&2\end{bmatrix} - \lambda I \right) = det\left(\begin{bmatrix}2 - \lambda&-1&0\-1&2 - \lambda&-1\0&-1&2-\lambda\end{bmatrix} \right) = -\lambda^3 + 6 \lambda^2 - 10\lambda + 4$$

CP(A) = 0 \Leftrightarrow \lambda = 2 \lor \lambda = 2 \pm \sqrt{2}

Therefore we have 3 eigenvalues and they are all positive, so A is positive definite and it is clearly symmetric as well.

Now we switch to the general proof for the monotonicity.

To prove that this is true, we first consider a way to express any iterate $x_k$ in function of the minimizer x_s and of the missing iterations:

x_k = x_s + \sum_{i=k}^{N} \alpha_i A^i p_0

This formula makes use of the fact that step directions in CG are all A-orthogonal with each other, so the k-th search direction p_k is equal to A^k p_0, where p_0 = -r_0 and r_0 is the first residual.

Given that definition of iterates, we're able to express the error after iteration k e_k in a similar fashion:

e_k = x_k - x_s = \sum_{i=k}^{N} \alpha_i A^i p_0

We then recall the definition of energy norm \|e_k\|_A:

\|e_k\|_A = \sqrt{\langle Ae_k, e_k \rangle}

We then want to show that \|e_k\|_A = \|x_k - x_s\|_A > \|e_{k+1}\|_A, which in turn is equivalent to claim that:

\langle Ae_k, e_k \rangle > \langle Ae_{k+1}, e_{k+1} \rangle

Knowing that the dot product is linear w.r.t. either of its arguments, we pull out the sum term related to the k-th step (i.e. the first term in the sum that makes up e_k) from both sides of \langle Ae_k, e_k \rangle, obtaining the following:

$$\langle Ae_{k+1}, e_{k+1} \rangle + \langle \alpha_k A^{k+1} p_0, e_k \rangle

• \langle Ae_{k+1},\alpha_k A^k p_0 \rangle > \langle Ae_{k+1}, e_{k+1} \rangle$$

which in turn is equivalent to claim that:

$$\langle \alpha_k A^{k+1} p_0, e_k \rangle

• \langle Ae_{k+1},\alpha_k A^k p_0 \rangle > 0$$

From this expression we can collect term \alpha_k thanks to linearity of the dot-product:

$$\alpha_k (\langle A^{k+1} p_0, e_k \rangle

• \langle Ae_{k+1}, A^k p_0 \rangle) > 0$$

and we can further "ignore" the \alpha_k term since we know that all $\alpha_i$s are positive by definition:

$$\langle A^{k+1} p_0, e_k \rangle

• \langle Ae_{k+1}, A^k p_0 \rangle > 0$$

Then, we convert the dot-products in their equivalent vector to vector product form, and we plug in the definitions of e_k and e_{k+1}:

$$p_0^T (A^{k+1})^T (\sum_{i=k}^{N} \alpha_i A^i p_0) + p_0^T (A^{k})^T (\sum_{i=k+1}^{N} \alpha_i A^i p_0) > 0$$

We then pull out the sum to cover all terms thanks to associativity of vector products:

$$\sum_{i=k}^N (p_0^T (A^{k+1})^T A^i p_0) \alpha_i+ \sum_{i=k+1}^N (p_0^T (A^{k})^T A^i p_0) \alpha_i > 0$$

We then, as before, can "ignore" all \alpha_i terms since we know by definition that they are all strictly positive. We then recalled that we assumed that A is symmetric, so A^T = A. In the end we have to show that these two inequalities are true:

p_0^T A^{k+1+i} p_0 > 0 \; \forall i \in [k,N]

p_0^T A^{k+i} p_0 > 0 \; \forall i \in [k+1,N]

To show these inequalities are indeed true, we recall that A is symmetric and positive definite. We then consider that if a matrix A is SPD, then A^i for any positive i is also SPD¹. Therefore, both inequalities are trivially true due to the definition of positive definite matrices.

Thanks to this we have indeed proven that the delta $|e_k|A - |e{k+1}|_A$ is indeed positive and thus as i increases the energy norm of the error monotonically decreases.

Question 2

Point 1

(a) For which kind of minimization problems can the trust region method be used? What are the assumptions on the objective function?

The trust region method is an algorithm that can be used for unconstrained minimization. The trust region method uses parts of the gradient descent and Newton methods, and thus it accepts basically the same domain of objectives that these two methods accept.

These constraints namely require the objective function f(x) to be twice differentiable in order to make building a quadratic model around an arbitrary point possible. In addition, our assumptions w.r.t. the scope of this course require that f(x) should be continuous up to the second derivatives. This is needed to allow the Hessian to be symmetric (as by the Schwartz theorem) which is an assumption that simplifies significantly proofs related to the method (like namely Exercise 3 in this assignment).

Finally, as all the other unconstrained minimization methods we covered in this course, the trust region method is only able to find a local minimizer close to he chosen starting points, and by no means the computed minimizer is guaranteed to be a global minimizer.

(b) Write down the quadratic model around a current iterate xk and explain the meaning of each term.

m(p) = f + g^T p + \frac12 p^T B p \;\; \text{ s.t. } \|p\| \leq \Delta

Here's an explaination of the meaning of each term:

• \Delta is the trust region radius, i.e. an upper bound on the step's norm (length);
• f is the energy function value at the current iterate, i.e. f(x_k);
• p is the trust region step, the solution of \arg\min_p m(p) with $|p| < \Delta$, i.e. the optimal step to take;
• g is the gradient at the current iterate x_k, i.e. \nabla f(x_k);
• B is the hessian at the current iterate x_k, i.e. \nabla^2 f(x_k).

(c) What is the role of the trust region radius?

The role of the trust region radius is to put an upper bound on the step length in order to avoid "overly ambitious" steps, i.e. steps where the the step length is considerably long and the quadratic model of the objective is low-quality (i.e. the performance measure \rho_k in the TR algorithm indicates significant energy difference between the true objective and the quadratic model).

In layman's terms, the trust region radius makes the method switch more gradient based or more quadratic based steps w.r.t. the "confidence" (measured in terms of \rho_k) in the computed quadratic model.

(d) Explain Cauchy point, sufficient decrease and Dogleg method, and the connection between them.

The Cauchy point and Dogleg method are algorithms to compute iteration steps that are in the bounds of the trust region. They allow to provide an approximate solution to the minimization of the quadratic model inside the TR radius.

The Cauchy point is a method providing sufficient decrease (as per the Wolfe conditions) by essentially performing a gradient descent step with a particularly chosen step size limited by the TR radius. However, since this method basically does not exploit the quadratic component of the objective model (the hessian is only used as a term in the step length calculation), even if it provides sufficient decrease and consequentially convergence it is rarely used as a standalone method to compute iteration steps.

The Cauchy point is therefore often integrated in another method called Dogleg, which uses the former algorithm in conjunction with a purely Newton step to provided a steps obtained by a blend of linear and quadratic information.

This blend is achieved by choosing the new iterate by searching along a path made out of two segments, namely the gradient descent step with optimal step size and a segment pointing from the last point to the pure netwon step. The peculiar angle between this two segments is the reason the method is nicknamed "Dogleg", since the final line resembles a dog's leg.

In the Dogleg method, the Cauchy point is used in case the trust region is small enough not to allow the "turn" on the second segment towards the Netwon step. Thanks to this property and the use of the performance measure \rho_k to grow and shrink the TR radius, the Dogleg method performs well even with inaccurate quadratic models. Therefore, it still satisfies sufficient decrease and the Wolfe conditions while delivering superlinear convergence, compared to the purely linear convergence of Cauchy point steps.

(e) Write down the trust region ratio and explain its meaning.

\rho_k = \frac{f(x_k) - f(x_k + p_k)}{m_k(0) - m_k(p_k)}

The trust region ratio and performance measure \rho_k measures the quality of the quadratic model built around the current iterate x_k, by measuring the ratio between the energy difference between the old and the new iterate according to the real energy function w.r.t. the quadratic model around x_k.

The ratio is used to test the adequacy of the current trust region radius. For an inaccurate quadratic model, the predicted energy decrease would be considerably higher than the effective one and thus the ratio would be low. When the ratio is lower than a predetermined threshold (\frac14 is the one chosen by Nocedal) the trust region radius is divided by 4. Instead, a very accurate quadratic model would result in little difference with the real energy function and thus the ratio would be close to 1. If the trust region radius is higher than a certain predetermined threshold (\frac34 is the one chosen by Nocedal), then the trust region radius is doubled in order to allow for longer steps, since the model quality is good.

(f) Does the energy decrease monotonically when Trust Region method is employed? Justify your answer.

In the trust region method the energy of the iterates does not always decrease monotonically. This is due to the fact that the algorithm could actively reject a step if the performance measure factor \rho_k is less that a given constant \eta. In this case, the new iterate is equal to the old one, no step is taken and thus the energy norm does not decrease but stays the same.

Point 2

The trust region algorithm is the following:

\begin{algorithm}[H] \SetAlgoLined Given \hat{\Delta} > 0, \Delta_0 \in (0,\hat{\Delta}), and $\eta \in [0, \frac14)$;

\For{$k = 0, 1, 2, \ldots$}{% Obtain p_k by using Cauchy or Dogleg method; $\rho_k \gets \frac{f(x_k) - f(x_k + p_k)}{m_k(0) - m_k(p_k)}$; \uIf{$\rho_k < \frac14$}{% $\Delta_{k+1} \gets \frac14 \Delta_k$; }\Else{% \uIf{\rho_k > \frac34 and $|\rho_k| = \Delta_k$}{% $\Delta_{k+1} \gets \min(2\Delta_k, \hat{\Delta})$; } \Else{% $\Delta_{k+1} \gets \Delta_k$; }} \uIf{$\rho_k > \eta$}{% $x_{k+1} \gets x_k + p_k$; } \Else{ $x_{k+1} \gets x_k$; } } \caption{Trust region method} \end{algorithm}

The Cauchy point algorithm is the following:

\begin{algorithm}[H] \SetAlgoLined Input B (quadratic term), g (linear term), $\Delta_k$; \uIf{$g^T B g \geq 0$}{% $\tau \gets 1$; }\Else{% $\tau \gets \min(\frac{|g|^3}{\Delta_k \cdot g^T B g}, 1)$; }

$p_k \gets -\tau \cdot \frac{\Delta_k}{|g|^2 \cdot g}$; \Return{$p_k$} \caption{Cauchy point} \end{algorithm}

Finally, the Dogleg method algorithm is the following:

\begin{algorithm}[H] \SetAlgoLined Input B (quadratic term), g (linear term), $\Delta_k$; $p_N \gets - B^{-1} g$;

\uIf{$\|p_N\| < \Delta_k$}{%
  $p_k \gets p_N$\;
}\Else{%
    $p_u = - \frac{g^T g}{g^T B g} g$\;

    \uIf{$\|p_u\| > \Delta_k$}{%
      compute $p_k$ with Cauchy point algorithm\;
    }\Else{%
        solve for $\tau$ the equality $\|p_u + \tau * (p_N - p_u)\|^2 =
        \Delta_k^2$\;
        $p_k \gets p_u + \tau \cdot (p_N - p_u)$\;
    }
}

\caption{Dogleg method} \end{algorithm}

Point 3

The trust region, dogleg and Cauchy point algorithms were implemented respectively in the files trust_region.m, dogleg.m, and cauchy.m.

Point 4

Taylor expansion

The Taylor expansion up the second order of the function is the following:

$$f(x_0, w) = f(x_0) + \langle\begin{bmatrix}48x^3 - 16xy + 2x - 2\2y - 8x^2 \end{bmatrix}, w\rangle + \frac12 \langle\begin{bmatrix}144x^2 -16y + 2 - 16 & -16 \ -16 & 2 \end{bmatrix}w, w\rangle$$

Minimization

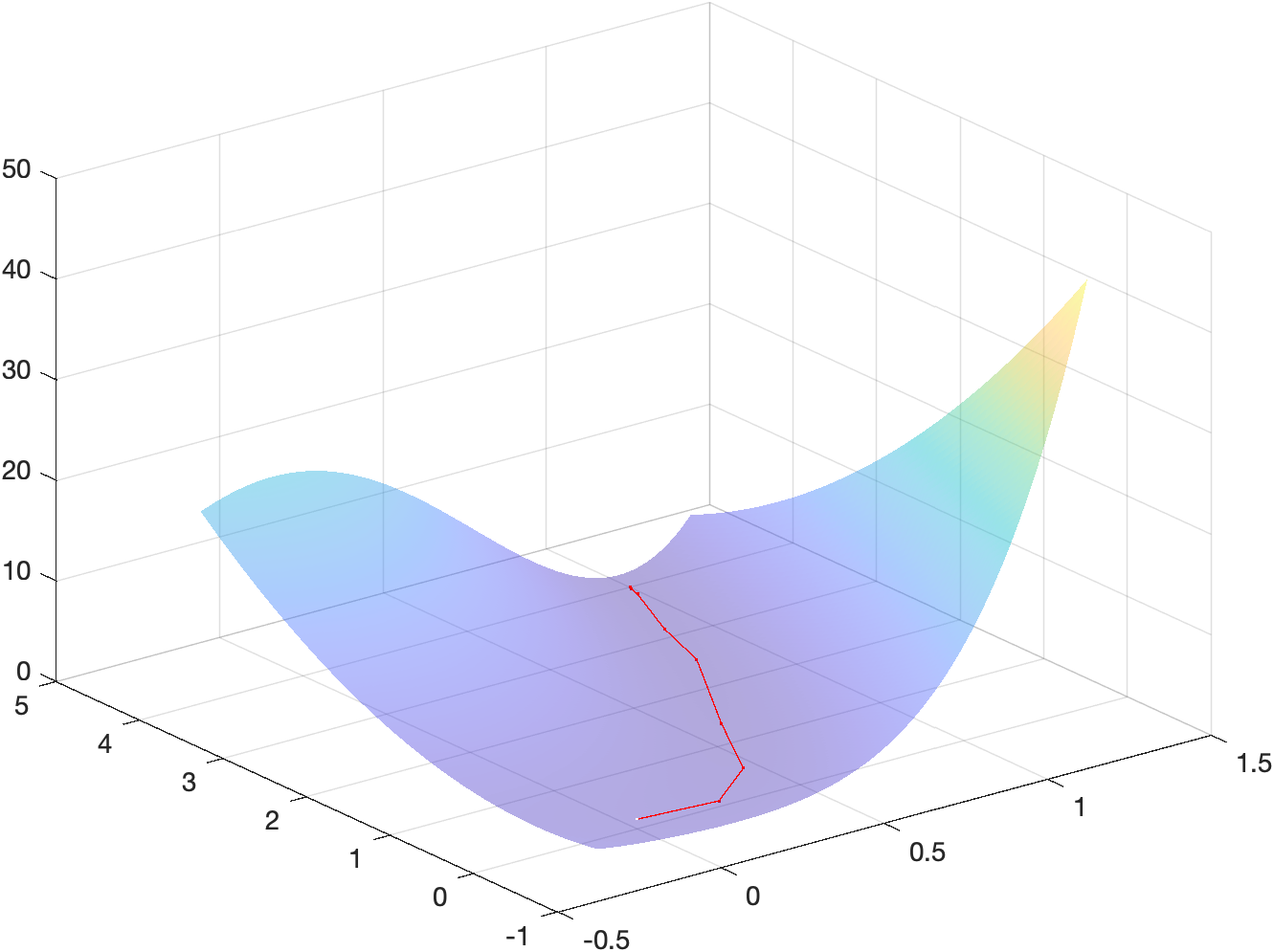
The code used to minimize the function can be found in the MATLAB script main.m under section 2.4. The resulting minimizer (found in 10 iterations) is:

x_m = \begin{bmatrix}1\\4\end{bmatrix}

Energy landscape

The following figure shows a surf plot of the objective function overlayed with the iterates used to reach the minimizer:

The code used to generate such plot can be found in the MATLAB script main.m under section 2.4c.

Point 5

Minimization

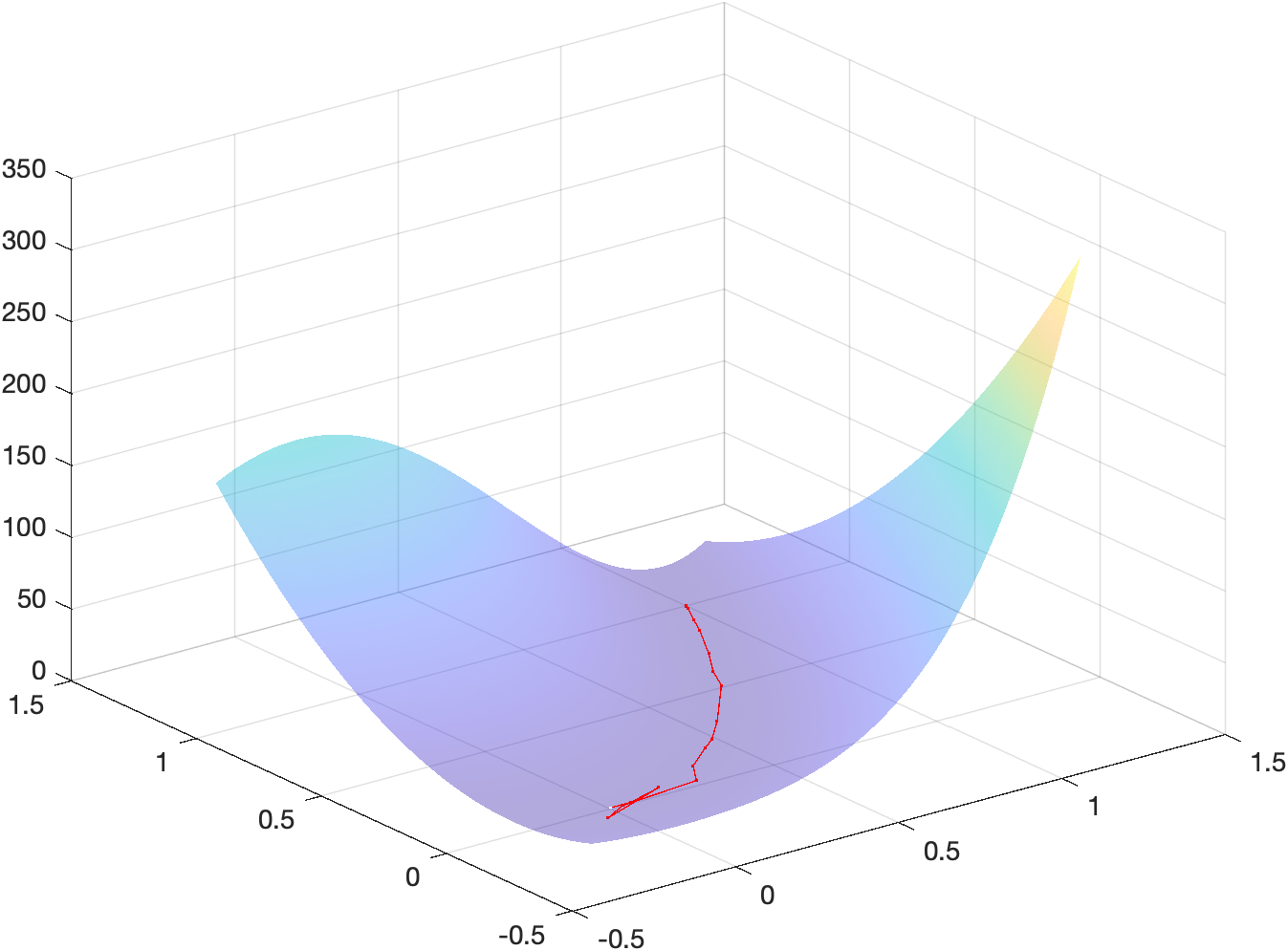
The code used to minimize the function can be found in the MATLAB script main.m under section 2.5. The resulting minimizer (found in 25 iterations) is:

x_m = \begin{bmatrix}1\\5\end{bmatrix}

Energy landscape

The following figure shows a surf plot of the objective function overlayed with the iterates used to reach the minimizer:

The code used to generate such plot can be found in the MATLAB script main.m under section 2.5b.

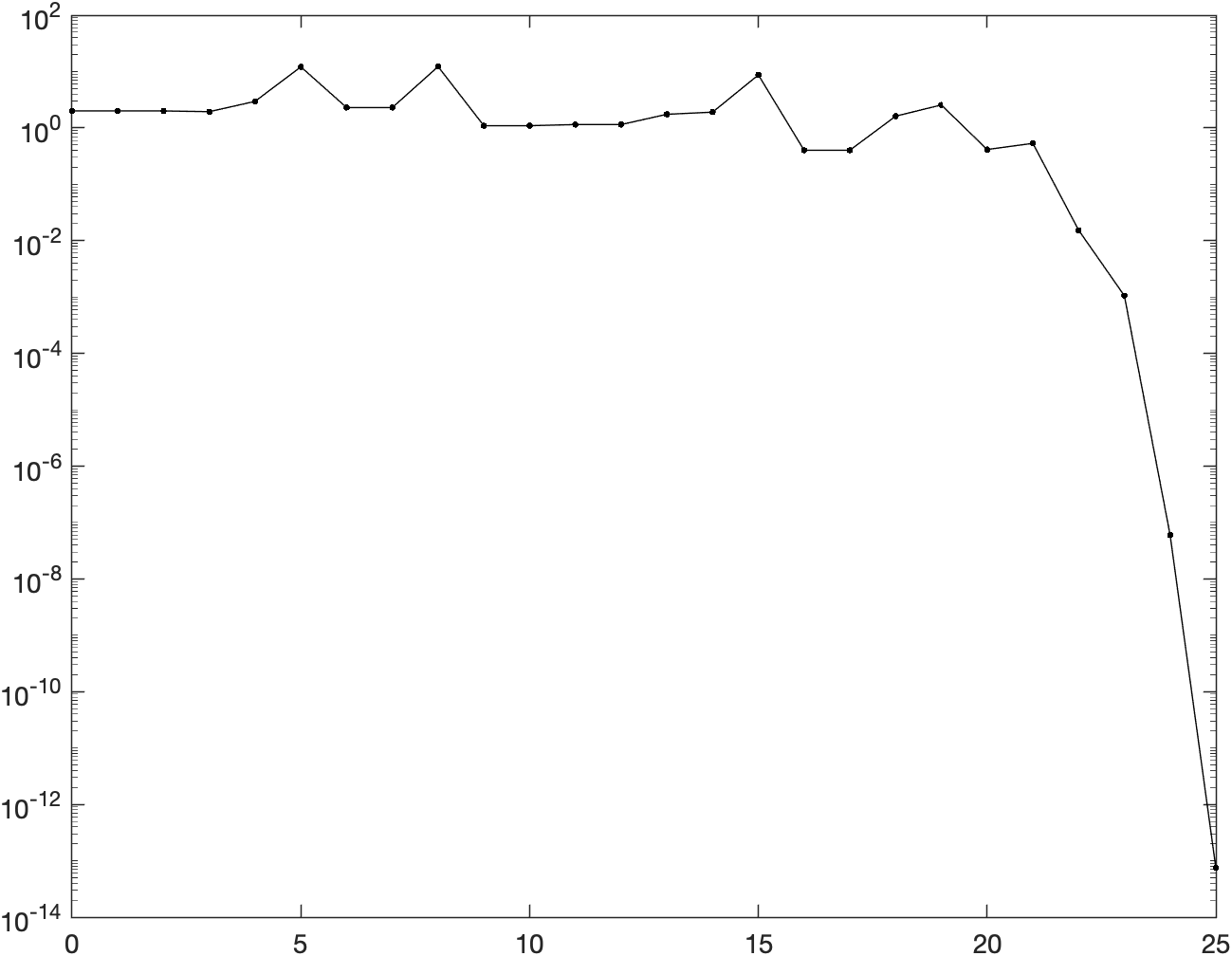
Gradient norms

The following figure shows the logarithm of the norm of the gradient w.r.t. iterations:

The code used to generate such plot can be found in the MATLAB script main.m under section 2.5c.

Comparing the behaviour shown above with the figures obtained in the previous assignment for the Newton method with backtracking and the gradient descent with backtracking, we notice that the trust-region method really behaves like a compromise between the two methods. First of all, we notice that TR converges in 25 iterations, almost double of the number of iterations of regular NM + backtracking. The actual behaviour of the curve is somewhat similar to the Netwon gradient norms curve w.r.t. to the presence of spikes, which however are less evident in the Trust region curve (probably due to Trust region method alternating quadratic steps with linear or almost linear steps while iterating). Finally, we notice that TR is the only method to have neighbouring iterations having the exact same norm: this is probably due to some proposed iterations steps not being validated by the acceptance criteria, which makes the method mot move for some iterations.

Exercise 3

We first show that the lemma holds for \tau \in [0,1]. Since

\|\tilde{p}(\tau)\| = \|\tau p^U\| = \tau \|p^U\| \text{ for } \tau \in [0,1]

Then the norm of the step \tilde{p} clearly increases as $\tau$ increases. For the second criterion, we compute the quadratic model for a generic \tau \in [0,1]:

$$m(\tilde{p}(\tau)) = f + g^T * \tilde{p}(\tau) + \frac{1}{2} \tilde{p}(\tau)^T B \tilde{p}(\tau) = f + g^T \tau p^U + \frac12 \tau (p^U)^T B \tau p^U

We then recall the definition of p^U:

 p^U = -\frac{g^Tg}{g^TBg}g: 

and plug it into the expression:

= f + g^T \tau \cdot - \frac{g^Tg}{g^TBg}g + \frac{1}{2} \tau \cdot -\left(\frac{g^Tg}{g^TBg}g\right)^T \cdot B \tau \cdot - \frac{g^Tg}{g^TBg}g $$ = f - \tau \cdot \frac{| g |^4}{g^TBg} + \frac{1}{2} \tau^2 \cdot \left(\frac{|g|^2}{g^T B g}\right) g^T \cdot B \frac{g^T g}{g^TBg}g $$ = f - \tau \cdot \frac{| g |^4}{g^TBg} + \frac{1}{2} \tau^2 \cdot \frac{| g |^4}{(g^TBg)^2} \cdot g^TBg $$ = f - \tau \cdot \frac{| g |^4}{g^TBg} + \frac{1}{2} \tau^2 \cdot \frac{| g |^4}{g^TBg} $$ = f + \left(\frac{1}{2} \tau^2 - \tau\right) \cdot \frac{| g |^4}{g^TBg}$$$$= f + \left(\frac12\tau^2 - \tau\right) z ; \text{where } z = \frac{| g |^4}{g^TBg}

We then compute the derivative of the model:

\frac{dm(\tilde{p}(\tau))}{d\tau} = z\tau - z = z(\tau - 1)

We know z is positive since g^T B g > 0, since we assume B is positive definite. Then, since \tau \in [0,1], the derivative is always \leq 0 and therefore we have proven that the quadratic model of the Dogleg step decreases as \tau increases.

Now we show that the two claims on gradients hold also for \tau \in [1,2]. We define a function h(\alpha) (where \alpha = \tau - 1) with same gradient "sign" as \|\tilde{p}(\tau)\| and we show that this function increases:

$$h(\alpha) = \frac12 |\tilde{p}(1 + \alpha)|^2 = \frac12 |p^U + \alpha(p^B - p^U)|^2 = \frac12 |p^U|^2 + \frac12 \alpha^2 |p^B - p^U|^2 + \alpha (p^U)^T (p^B - p^U)

We now take the derivative of h(\alpha) and we show it is always positive, i.e. that h(\alpha) has always positive gradient and thus that it is increasing w.r.t. \alpha:

$$h'(\alpha) = \alpha |p^B - p^U|^2 + (p^U)^T (p^B - p^U) \geq (p^U)^T (p^B - p^U) = \frac{g^Tg}{g^TBg}g^T\left(- \frac{g^Tg}{g^TBg}g + B^{-1}g\right) =$$$$= |g|^2 \frac{g^TB^{-1}g}{g^TBg}\left(1 - \frac{|g|^2}{(g^TBg)(g^TB^{-1}g)}\right)

Since we know B is symmetric and positive definite, then B^{-1} is as well. Therefore, we know that the term outside of the parenthesis is always positive or 0. Therefore, we now only need to show that:

$$\frac{|g|^2}{(g^TBg)(g^TB^{-1}g)} \leq 1 \Leftrightarrow |g|^2 \leq (g^TBg)(g^TB^{-1}g)

since both factors in the denominator are positive for what we shown before.

We now define a inner product space $\forall a, b \in R^N, ; {\langle a, b\rangle}_B = a^T B b$. We now prove that this is indeed a linear product space by proving all properties of such space:

• Linearity w.r.t. the first argument:

  $\alpha {\langle x, y \rangle}_B + \beta {\langle z, y \rangle}_B = \alpha \cdot x^TBy + \beta \cdot z^TBy = (\alpha x + \beta z)^TBy = {\langle (\alpha x + \beta z), y \rangle}_B$;

• Symmetry:

  {\langle x, y \rangle}_B = x^T B y = (x^T B y)^T = y^TB^Tx, and since B is symmetric, y^TB^Tx = y^TBx = {\langle y,x \rangle}_B;

• Positive definiteness:

  {\langle x, x \rangle_B} = x^T B x > 0 is true since B is positive definite for all x \neq 0.

Since {\langle x, y \rangle}_B is indeed a linear product space, then:

$${\langle g, B^{-1} g \rangle}_B \leq {\langle g, g \rangle}_B {\langle B^{-1} g, B^{-1} g \rangle}_B$$

holds according to the Cauchy-Schwartz inequality. Now, if we expand each inner product we obtain:

g^T B B^{-1} g \leq (g^T B g) (g^T (B^{-1})^T B B^{-1} g)

Which, since B is symmetric, in turn is equivalent to writing:

g^T g \leq (g^TBg) (g^T B^{-1} g)

which is what we needed to show to prove that the first gradient constraint holds for \tau \in [1,2].

For the second constraint, we adopt a similar strategy as for before and we define a new function \hat{h}(\alpha) = m(\tilde{p}(1 + \alpha)), thus plugging the Dogleg step in the quadratic model:

$$\hat{h}(\alpha) = m(\tilde{p}(1+\alpha)) = f + g^T (p^U + \alpha (p^B - p^U)) + \frac12 (p^U + \alpha (p^B - p^U))^T B (p^U + \alpha (p^B - p^U)) = $$ = f + g^T p^U + \alpha g^T (p^B - p^U) + \frac12 (p^U)^T B p^U + \frac12 \alpha (p^U)^T B (p^B - p^U) + \frac12 \alpha (p^B - p^U)^T B p^U + \frac12 \alpha^2 (p^B - p^U)^T B (p^B - p^U)

We now derive \hat{h}(\alpha):

$$\hat{h}'(\alpha) = g^T (p^B - p^U) + \frac12 (p^U)^T B (p^B - p^U) + \frac12 (p^B - p^U)^T B p^U + \alpha (p^B - p^U)^T B (p^B - p^U) = $$$$ = (p^B - p^U)^T g + \frac12 ((p^U)^T B (p^B - p^U))^T + \frac12 (p^B - p^U)^T B p^U + \alpha (p^B - p^U)^T B (p^B - p^U) = $$$$ = (p^B - p^U)^T g + \frac12 (p^B - p^U) B^T (p^U)^T + \frac12 (p^B - p^U)^T B p^U + \alpha (p^B - p^U)^T B (p^B - p^U) = $$$$ = (p^B - p^U)^T (g + \frac12 \cdot 2 \cdot B p^U) + \alpha (p^B - p^U)^T B (p^B - p^U) \leq $$$$ \leq (p^B - p^U)^T(g + B p^U + B (p^B - p^U)) = $$$$ =(p^B - p^U)^T(g+Bp^B) = $$$$ =(p^B - p^U)^T(g+B \cdot (-1) \cdot B^{-1} g) = $$$$ =(p^B - p^U)^T(g - g) = 0$$

and we therefore obtain \hat{h}(\alpha) \leq 0, thus finding that the m(\tilde{p}) is indeed a decreasing function of \tau or $\alpha = \tau - 1$ also for \tau \in [1,2], thus completing the proof for the lemma.

---

1. source: Wikipedia - Definite Matrix \to Properties $\to$ Multiplication ↩︎